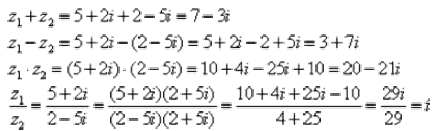Понятие комплексного числа
Содержание страницы:
Лекция 1. Понятие комплексного числа
Комплексным числом z называется число вида z = a + bi , где a и b – действительные числа, i – так называемая мнимая единица. Число a называется
действительной частью (Re z) ) комплексного числа z , число b называется мнимой частью (Im z) ) комплексного числа z . a + bi – это единое число, а не сложение.
Действительную и мнимую части комплексного числа, в принципе, можно переставить местами: z = b + ai или переставить мнимую единицу: z = a + ib – от этого комплексное число не изменится. Но стандартно комплексное число принято записывать именно в таком порядке: z = a + bi
Приведем геометрическую интерпретацию. Комплексные числа изображаются на комплексной плоскости:
Множество же комплексных чисел принято обозначать «жирной» или утолщенной буквой С. Поэтому на чертеже следует поставить букву С, обозначая тот факт, что у нас комплексная плоскость.
Комплексная плоскость состоит из двух осей:
Re z – действительная ось
Im z – мнимая ось
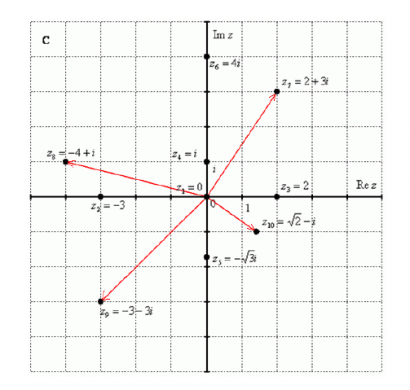
Построим на комплексной плоскости следующие комплексные числа:
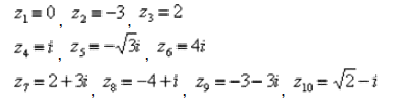
Алгебраическая форма комплексного числа.
Сложение, вычитание, умножение и деление комплексных чисел
С алгебраической формой комплексного числа мы уже познакомились, z = a + bi – это и есть алгебраическая форма комплексного числа.
Действия с комплексными числами не представляют особых сложностей и мало чем отличаются от обычной алгебры.
Сложение комплексных чисел
Пример 1 Сложить два комплексных числа 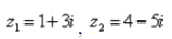
Для того чтобы сложить два комплексных числа нужно сложить их действительные и мнимые части: 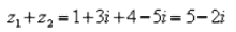
Таким способом можно найти сумму любого количества слагаемых: просуммировать действительные части и просуммировать мнимые части.
Для комплексных чисел справедливо правило первого класса: 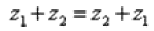 – от перестановки слагаемых сумма не меняется.
– от перестановки слагаемых сумма не меняется.
Вычитание комплексных чисел
Пример 2 Найти разности комплексных чисел 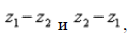 если
если 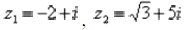
Действие аналогично сложению, единственная особенность состоит в том, что вычитаемое нужно взять в скобки, а затем – стандартно раскрыть эти скобки со сменой знака:
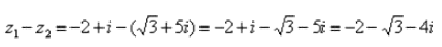
Результат не должен смущать, у полученного числа две, а не три части. Просто действительная часть – составная: 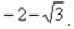 Для наглядности ответ можно переписать так:
Для наглядности ответ можно переписать так: 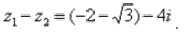
Рассчитаем вторую разность:
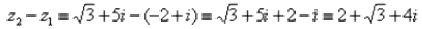
Здесь действительная часть тоже составная: 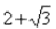
Чтобы не было какой-то недосказанности, приведу короткий пример с «нехорошей» мнимой частью: 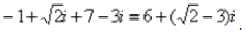 Вот здесь без скобок уже не обойтись.
Вот здесь без скобок уже не обойтись.
Умножение комплексных чисел
Для умножения важно помнить, что 
Пример 3 Найти произведение комплексных чисел 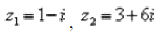
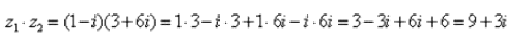
Как и сумма, произведение комплексных чисел перестановочно, то есть справедливо равенство: 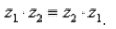
Деление комплексных чисел
Пример 4 Даны комплексные числа 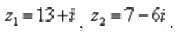 Найти частное
Найти частное 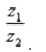
Составим частное:
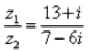
Деление чисел осуществляется методом умножения знаменателя и числителя на сопряженное знаменателю выражение.
Вспоминаем формулу (a — b)(a + b) = a2 — b2 и смотрим на наш знаменатель: 7 — 6i . В знаменателе уже есть (a — b) , поэтому сопряженным выражением в данном случае является (a + b) , то есть 7 + 6i
Согласно правилу, знаменатель нужно умножить на 7 + 6i , и, чтобы ничего не изменилось, домножить числитель на то же самое число 7 + 6i:
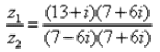
Распишем подробнее 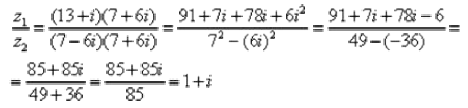
В ряде случаев перед делением дробь целесообразно упростить, например, рассмотрим частное чисел: 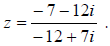
Перед делением избавляемся от лишних минусов: в числителе и в знаменателе выносим минусы за скобки и сокращаем эти минусы: 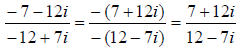
Пример 5 Дано комплексное число 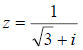 . Записать данное число в алгебраической форме (т.е. в форме a + bi ).
. Записать данное число в алгебраической форме (т.е. в форме a + bi ).
Приём тот же самый – умножаем знаменатель и числитель на сопряженное знаменателю выражение. Знаменатель и числитель нужно домножить на сопряженное выражение на 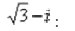
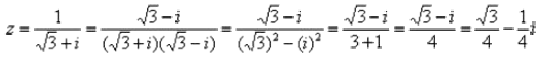
Пример 6 Даны два комплексных числа 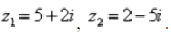 Найти их сумму, разность, произведение и частное.
Найти их сумму, разность, произведение и частное.