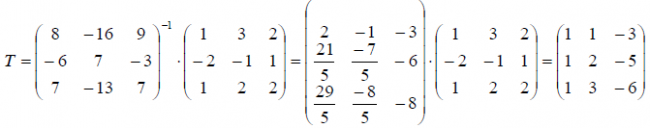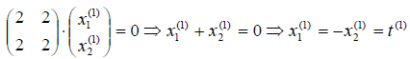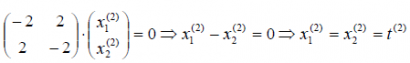Замена базиса
Содержание страницы:
Лекция 7. Замена базиса
Матрица преобразования координат
Возьмём в пространстве En два различных базиса e1,e2,…,en и E1,E2,…,En
Рассуждение проведём для случая n = 3. Один и тот же вектор x относительно различных базисов имеет различные координаты. Можем написать:
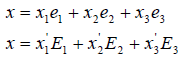
Любой вектор второго базиса можем разложить по первому базису, т.е.
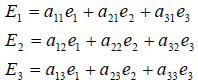
Подставим:
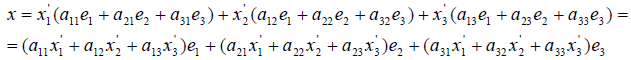
В силу единственности разложения по данному базису мы должны приравнять коэффициенты при векторах e1,e2,e3 и полученные. Тогда
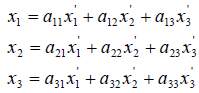
Введём в рассмотрение матрицы
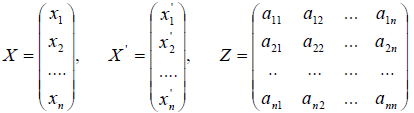
Тогда полученные соотношения можно записать в матричном виде X = Z X .
Матрица Z называется матрицей преобразование координат при переходе от старого базиса к новому, т.е. от базиса e1,e2,…,en к базису E1,E2,…,En . Причём, столбцами матрицы преобразования координат являются координаты вектора нового базиса E1,E2,…,En относительно старого базиса e1,e2,…,en .
Изменение матрицы линейного оператора при переходе к новому базису
Пусть в пространстве En определён линейный оператор A , т.е. y = A x
Или Y = A X , где X (x1,x2,…,xn)T и Y (y1,y2,…,yn)T матрицы-столбцы, составленные из координат векторов x и y относительно данного базиса n1,e2,…,en , A — матрица линейного оператора A .
Выберем в том же пространстве En другой базис E1,E2,…,En . Относительно нового базиса матрица линейного оператора A будет иной. Обозначим через T матрицу преобразования координат, а через X и Y — одностолбцовые матрицы, составленные из координат векторов x и y относительно нового базиса, т.е.
X = T X ,
Y = T Y
Подставим полученное в общий вид, тогда получим: T Y = A T X
Умножая левую и правую части равенства слева на T-1 , получим: Y = T-1 A T X .
Итак, если в En перейти к новому базису, то матрица линейного оператора также изменится и в самом общем случае будет равна T-1 A T .
Пример: Оператор A в базисе пространства E3
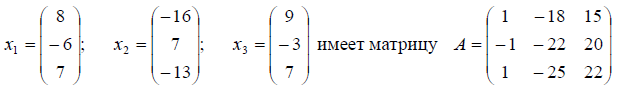
Найти его матрицу в базисе
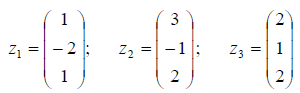
Решение: Матрица оператора в новом базисе находим по формуле B = T-1AT , где T — матрица перехода от старого базиса к новому. Матрицу перехода находим по формуле T = X-1 Y .
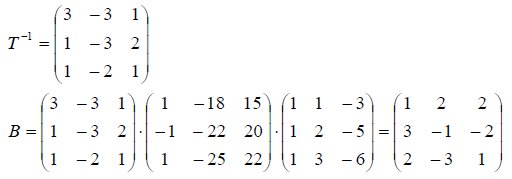
Сопряженный и самосопряженный оператор
Пусть в вещественном евклидовом пространстве En определён линейный оператор A
Определение 1. Оператор A* в вещественном евклидовом пространстве En называется сопряженным по отношению к линейному оператору A в том же пространстве, если его матрица в любом ортонормированном базисе этого пространства является транспонированной по отношению к матрице оператора A .
Свойства сопряженного оператора
1. E* = E, где E — тождественный оператор, т.е. оператор, матрица которого E единичная в En
2. (A + B)* = A* + B*
3. (A B)* = B* A*
4. если A-1 существует, то (A-1)* = (A*)-1 .
Определение 2. Линейный оператор A, определённый в вещественном евклидовом пространстве En, называется самосопряженным, или симметрическим, если он cовпадает со своим сопряженным оператором A* , т.е. если A* = A .
Матрица самосопряженного оператора совпадает с транспонированной в любом ортонормированном базисе, т.е. является симметричной относительно главной диагонали.
Свойства самосопряженного оператора
1. если A* = A , B* = B , то (A + B)* = A* + B* = A + B ;
2. если A — невырожденный самосопряженный оператор, то (A-1)* = (A*)-1 = A-1 .
Доказательство. Действительно, если существует A-1 и кроме того A* = A , то в силу свойства 4 сопряженного оператора, получим (A-1)* = (A*)-1 = A-1 ;
3. Если A — самосопряженный оператор в вещественном пространстве En, то имеет место равенство: 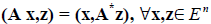
Собственные векторы и собственные значения линейного оператора
Пусть A — линейный оператор. Пусть x 1, где 1 некоторое подпространство пространства En. Вектор y = A x может принадлежать подпространству 1, а может и не принадлежать.
Определение. Подпространство 1 называется инвариантным по отношению к оператору A, если A x 1, x 1.
Определение. Ненулевой вектор x называется собственным вектором линейного оператора A, если найдётся такое число , что будет выполняться равенство A x = x . При этом число называют собственным значением (собственным числом) оператора A, соответствующим вектору x. Множество всех собственных значений оператора A называется его спектром.
Остановимся на отыскании собственных значений и собственных векторов линейного оператора A. Рассмотрение проведём для случая n = 3. Итак, пусть в некотором базисе оператор A имеет матрицу
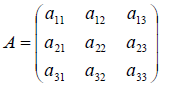
и пусть одностолбцовая матрица 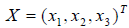 соответствует вектору x. Тогда в силу определения
соответствует вектору x. Тогда в силу определения
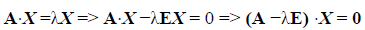
Дело свелось к решению системы линейных однородных уравнений, записанной в матричном виде. Очевидно, что эта система имеет ненулевое решение, если det(A E) = 0. Уравнение det(A E) = 0 называется характеристическим уравнением оператора A; многочлен det(A E) называется соответственно характеристическим многочленом оператора A. В координатной форме характеристическое уравнение выглядит так:
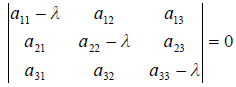
Решив его, найдём 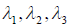 — собственные значения линейного оператора. Далее, для суммы диагональных элементов матрицы A, которую называют следом этой матрицы trA или следом оператор A (trA), справедлива формула
— собственные значения линейного оператора. Далее, для суммы диагональных элементов матрицы A, которую называют следом этой матрицы trA или следом оператор A (trA), справедлива формула 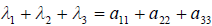 . Кроме того, detA = 1 2 3.
. Кроме того, detA = 1 2 3.
После того как найдены собственные значения линейного оператора A, остаётся подставить их по очереди в уравнение и найти соответствующие собственные векторы x(1), x(2), x(3)
Пример: Найти собственные значения и собственные числа линейного оператора, матрица которого
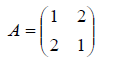
Решение. По определения собственного вектора можем написать 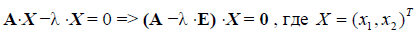 — матрица – столбец, соответствующая искомому вектору x линейного оператора A;
— матрица – столбец, соответствующая искомому вектору x линейного оператора A;
В матричной форме получим:
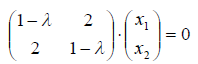
Система однородная, следовательно, она имеет бесчисленное множество решений, если определитель системы равен нулю, т.е. имеем характеристическое уравнение:
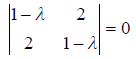
Решая его, получим такие собственные значения 1 = 1; 2 = 3.
Найдём соответствующие собственные векторы.
1) 1 = 1 подставим в уравнение, получим
где t(1) — некоторый параметр. Таким образом, имеем множество коллинеарных векторов, соответствующих первому собственному числу 1 = 1:
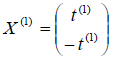
Этот вектор нетрудно пронормировать, тогда мы получим единичный собственный вектор, соответствующий первому собственному числу 1 = 1 т.е.
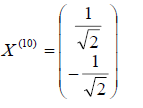
2) 2 = 3 подставим в уравнение, получим
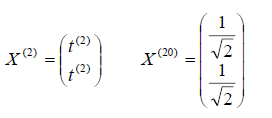
В заключение заметим, что множество всех векторов y = A x , где x En, называется областью значений линейного оператора A в En, а множество всех векторов x 1 En, таких, что A x = 0, называется ядром линейного оператора.
Свойства собственных чисел и собственных векторов самосопряженного оператора
Рассмотрим самосопряженный оператор A, определённый в вещественном евклидовом пространстве En. В силу определения матрица его A -симметрическая.
Теорема 1. Собственные числа самосопряженного оператора A есть вещественные числа.
Теорема 2. Собственные векторы, отвечающие двум различным собственным значениям самосопряженного оператора, ортогональны.
>Доказательство. Пусть 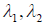 — различные собственные значения самосопряженного оператора A, а x1, x2 — соответствующие им собственные значения. Тогда
— различные собственные значения самосопряженного оператора A, а x1, x2 — соответствующие им собственные значения. Тогда
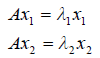
Следовательно,
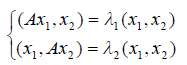
Но 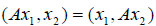 т.е. левые части равенств равны, следовательно, вычитая их почленно, получим:
т.е. левые части равенств равны, следовательно, вычитая их почленно, получим: 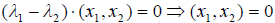 а это и означает, что собственные векторы x1, x2 ортогональны.
а это и означает, что собственные векторы x1, x2 ортогональны.
Замечание. Так как собственные векторы самосопряженного оператора A ортогональны, их можно принять за базис линейного пространства, в котором определён этот линейный оператор. Поделив далее каждый вектор на его длину, мы получаем ортонор мированный базис.
Теорема 3. В базисе из единичных собственных векторов самосопряженного оператора матрица этого оператора диагональная, причём элементами диагонали являются её собственные числа.
Доказательство. Доказательство проведём для случая n = 3. Пусть e1, e2, e3 — единичные векторы самосопряженного оператора A относительно некоторого базиса линейного пространства 3, отвечающие собственным значениям 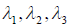 этого линейного оператора, т.е.
этого линейного оператора, т.е. 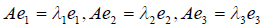 . Примем векторы e1, e2, e3 за базис линейного пространства. Очевидно, что в этом базисе векторы
. Примем векторы e1, e2, e3 за базис линейного пространства. Очевидно, что в этом базисе векторы 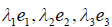 имеют координаты:
имеют координаты:
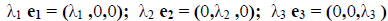 . Следовательно, матрица A оператора A в базисе e1, e2, e3 имеет вид:
. Следовательно, матрица A оператора A в базисе e1, e2, e3 имеет вид:
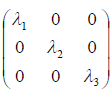
Выбор такого базиса, в котором матрица линейного оператора имеет диагональный вид, называется приведением матрицы к диагональному виду.