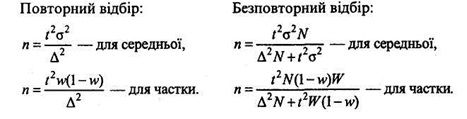ТЕМА 7. Вибіркове спостереження у правовій статистиці
Зміст сторінки:
ТЕМА 7. Вибіркове спостереження у правовій статистиці
1. Теоретичні основи вибіркового методу
2. Способи відбору у вибіркову сукупність
1.
Теоретичні основи вибіркового методу
Основного формою збору інформації з різноманітних питань юриспруденції є
державна статистична звітність правоохоронних та інших юридичних установ.
Звітність включає найважливіші показники правової діяльності. Оскільки
дійсність швидко змінюється і на актуальні питання відповіді в офіційній
статистичній звітності немає, юридична наука і практика систематично потребують
інформації, що відображає цю дійсність. Таку інформацію можна одержати
вибірковим спостереженням.
Методика вибіркового спостереження досконало розроблена математичною
статистикою. Воно широко застосовується в різних галузях науки і практики як
метод, який в багатьох випадках замінює суцільне вивчення тих чи інших явищ та
процесів.
Вибірковий метод відносно простий, економічний, оперативний, надійний і має
достатньо визначену точність.
Теорія вибіркового спостереження базується на статистичних закономірностях,
які формуються і виявляються в масових явищах та процесах. Ця властивість
закономірностей отримала назву закону
великих чисел. Математичною основою закону великих чисел є теорія ймовірності.
Вибіркове спостереження – науково
обґрунтований вид несуцільного спостереження, при якому обстежується частина
одиниць досліджуваної сукупності, відібрана за певними правилами, що дає змогу
на підставі вибіркових оцінок отримати дані для характеристики сукупності в
цілому.
Отже, при вибірковому спостереженні обстежується визначена, заздалегідь
обумовлена частина сукупності 1/10; 1/20; 1/50 та ін., а результати поширюються
на всю сукупність.
Вибіркове спостереження набуло поширення, тому що має ряд переваг порівняно з суцільним спостереженням:
• потребує значно менше витрат праці, засобів, коштів, ніж суцільне спостереження;
• оперативніше за суцільне спостереження;
• дає змогу чіткіше організувати і провести спостереження і цим забезпечити
більш точні результати, ніж при суцільному спостереженні дуже великої
сукупності;
• дає можливість розширити програму спостережень і значно доповнити дані,
отримані в результаті суцільного спостереження;
• може застосовуватися, коли неможливо провести суцільне спостереження
через великий обсяг сукупності або тому, що в результаті дослідження одиниці
спостереження знищуються або псуються.
Причини проведення вибіркового
спостереження:
–
неможливість суцільного спостереження;
– значні
затрати на його виконання;
– стислі
терміни обробки даних;
– перевірка
результатів суцільного спостереження.
При вибірковому спостереженні мають справу з двома категоріями
узагальнених показників: відносними і середніми. Відносні величини застосовуються для зведеної характеристики
сукупності за альтернативними ознаками. Така характеристика дається у вигляді
частки тих одиниць сукупності, що мають досліджувану ознаку (частка засуджених
строком на 5 років і більше; частка засуджених, що мають вищу освіту; частка
засуджених, що мають сім’ї і та. ін.). Узагальнюючими характеристиками
сукупності за кількісною ознакою є середнівеличини.
Уся сукупність одиниць, із яких відбирають певну частину для вибіркового
спостереження, називається генеральною сукупністю. Узагальнені показники
генеральної сукупності називаються генеральними. Частина одиниць, відібраних
для вибіркового спостереження, називається вибірковою сукупністю, а
узагальнені показники – вибірковими.
Але незалежно від того яким чином проводився відбір до сукупності, завжди
будуть розбіжності між характеристиками генеральної та вибіркової сукупності,
пов’язані із сутністю вибіркового методу.
Відповідь на питання, наскільки велика і ймовірна різниця між узагальненими
генеральними і вибірковими показниками, дає теорія вибіркового спостереження,
яка базується на законі великих чисел. Закон
великих чисел, що випливає з теорії П.Чебишева щодо вибіркового
спостереження, можна сформулювати так: з
імовірністю, як завгодно близькою до одиниці, можна стверджувати, що при
достатньо великій кількості спостережень зведені характеристики вибіркової
сукупності як завгодно мало відрізнятимуться від зведених характеристик генеральної
сукупності.
Точність результатів вибіркових досліджень багато разів перевірялась. Ці
спостереження підтвердили, що результати досліджень, проведених вибірковим
методом, дають досить точне уявлення про досліджувану сукупність і широко застосовуються
на практиці.
2.
Способи відбору у вибіркову сукупність
Найважливішою умовою проведення
вибіркового спостереження є правильний відбір одиниць сукупності:
• достатня кількість відібраних одиниць;
• об’єктивний відбір, що забезпечує однакову можливість кожній одиниці
сукупності потрапити у вибірку.
Вибіркова сукупність повинна бути утворена на основі випадкового відбору.
Розрізняють такі основні види відбору:
• власне-випадковий;
• механічний;
• розшарований.
За кількістю охоплених одиниць сукупності розрізняють великі і малі вибірки.
Власне-випадковий відбір полягає у тому, що спостереження ведеться за
частиною одиниць сукупності, відібраною з усієї сукупності у випадковому
порядку, ненавмисно. Випадковий відбір дає лотерея або жеребкування. На кожну
одиницю сукупності заготовляють жетон, квиток із номером. Потім у випадковому
порядку відбирають необхідну кількість жетонів (одиниць сукупності).
Випадкова вибірка може бути повторною і безповторною.
Повторним називається такий відбір, при якому
кожна одиниця сукупності бере участь у відборі стільки разів, скільки
відбирається одиниць.
Безповторний – це відбір, при якому відібрана
одиниця надалі не бере участі у відборі.
Механічний відбір полягає у тому, що вся
сукупність одиниць розбивається на рівні за обсягом групи з випадковими
ознаками, потім із кожної групи, як правило, випадковим порядком відбирається
одна одиниця. Механічний відбір – різновид власне-випадкового відбору, але
має ряд організаційних переваг (легше і простіше організувати перевірку
відбору одиниць сукупності).
Він буває тільки безповторним і організується у такий спосіб. Наприклад,
потрібно з 1000 засуджених відібрати 100 для вивчення залежності тяжкості
злочину від наявності освіти. Складають алфавітні списки всіх засуджених.
Визначають інтервал, що дорівнює 10 (1000 / 100). За складеним списком,
починаючи з будь-якого номера, у межах першого десятка відбирають у випадковому
порядку одного злочинця. Якщо з першого десятка випадковим добором відібрали
засудженого під номером 5, то далі відбирають 15-го, 25-го, 35-го і т. д.
Механічний відбір можна також застосувати, використовуючи природний Порядок
розташування одиниць генеральної сукупності (розподіл засуджених на ланки,
групи тощо).
Розшарований відбір починають з групування всієї
сукупності на якісно однорідні групи за істотною, типовою ознакою (наприклад,
групування засуджених за видами злочинів, статтями КК, місцем скоєння злочинів).
Потім із кожної групи власне-випадковим або механічним способом відбирають
кількість одиниць пропорційно питомій вазі групи в усій сукупності.
Розшарований відбір доцільно застосовувати при великій міжгруповій варіації.
При цьому відборі досягається більш повне представництво у вибірці окремих
типів досліджуваного явища, тому він дає точніші результати, ніж власне-випадковий
і механічний.
Крім того, у правовій статистиці використовують і такі види відбору, як
серійний, моментний, багатоступеневий, багатофазовий. Різні форми організації
відбору, як одиниць у вибіркову сукупність – це подальший розвиток та видозміна
простого випадкового відбору. Застосування того чи іншого виду відбору
визначається особливим характером об’єкта спостереження з метою здешевлення
або полегшення процесу спостереження.
3.
Помилки вибірки
Відхилення узагальнених показників вибіркової сукупності від зведених
характеристик генеральної сукупності називається помилками вибірки, вони
виникають внаслідок самого факту відбору. Структура вибіркової сукупності не
може точно відтворити генеральну сукупність. Помилки властиві вибірковому
спостереженню називаються помилками вибірки, або репрезентативності. За своєю
природою вони можуть бути систематичними і випадковими.
Систематичні помилки вибірки виникають
при порушенні принципів проведення вибіркового спостереження. Наприклад, якщо
при обстеженні успішності студентів відібрати для спостереження сильну групу,
то середній бал буде завищений.
Систематичні помилки спрямовані тільки в один бік (або зменшення, або
збільшення) і призводять до того, що вибіркове спостереження втрачає свій
сенс, тому що на його основі не можна правильно визначити показники
генеральної сукупності. Систематичних помилок можна уникнути. Для попередження
й усунення їх потрібно встановити науково обґрунтований порядок відбору, який
проводиться випадковим методом, коли кожній одиниці генеральної сукупності
забезпечена однакова можливість потрапити у вибірку.
Якщо відбір зроблено правильно, то розбіжності між узагальненими
показниками вибіркової і генеральної сукупностей виникають через сам факт
відбору і називаються випадковими помилками вибірки.
Випадкові помилки дають відхилення як в один, так і в інший бік. Вони
властиві вибірковому спостереженню, усунути їх практично неможливо, але можна
обчислити.
Помилка вибірки залежить від чисельності вибіркової сукупності і ступеня
варіації досліджуваної ознаки. Чим більше одиниць відібрано у вибіркову сукупність,
тим меншими, за інших рівних умов, будуть розбіжності. Чим менша варіація
ознаки, тим менша помилка вибірки.
В
математиці було доведено, що
де
– середня похибка вибірки; 2 – дисперсія ознаки в генеральній сукупності; n – число одиниць вибіркової
сукупності; N – число одиниць генеральної сукупності; w – частка
одиниць, що мають певні ознаки.
Із
наведених формул впливає, що похибка репрезентативності залежить від багатьох
чинників: ймовірності, з якою ми бажаємо отримати результат; кількості одиниць
вибіркової сукупності (чим менше одиниць складатиме вибіркова сукупність, тим
більше буде похибка репрезентативності, і навпаки); однорідності досліджуваної
сукупності (чим більше різнорідною є сукупність, тим більше буде похибка репрезентативності)
і від способу відбору одиниць у вибіркову сукупність.
Для визначення середньої помилки вибірки
потрібно знати дисперсію ознаки в генеральній сукупності. Але при
вибірковому спостереженні генеральна дисперсія невідома.
У курсі математичної статистики доведено, що
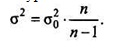
У міру зростання числа вибірки коефіцієнт
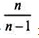
наближається до одиниці і розбіжності між генеральною і
вибірковою дисперсіями стають меншими. Тому середню помилку вибірки можна
обчислити, виходячи зі значення вибіркової дисперсії.
Середня помилка вибірки характеризує міру відхилень вибіркової середньої
від генеральної середньої, частки вибіркової від частки генеральної.
Розраховану за вказаними формулами помилку вибірки дає можливість
стверджувати, що показник вибіркової сукупності будуть відрізнятися від
показників генеральної сукупності на розраховану величину з імовірністю 0,683,
тобто якщо буде відібрано 1000 одиниць сукупності, то 683 із них матимуть дану
ознаку. Точність розрахунку можна гарантувати на 68,3 %.
Розраховані з імовірністю 0,683 показники не завжди влаштовують
дослідників. Щоб підвищити ймовірність, потрібно розширити межі відхилень і
вводиться довірчий коефіцієнт t. Середня помилка вибірки помножена на
довірчий коефіцієнт називається граничною помилкою вибірки.
Отже, гранична помилка вибірки розраховується за такою
формулою:
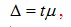
де
– похибка вибірки, тобто похибка репрезентативності;
–
середня похибка вибірки;
t –
коефіцієнт, що залежить від ймовірності, з якою можна гарантувати певний розмір
похибки репрезентативності.
Коефіцієнт довіри залежить від імовірності, з якою можна гарантувати, що
гранична помилка вибірки не перевищить t-кратну середню помилку. Коефіцієнт tвизначається за таблицями значень інтеграла ймовірностей. Так, при
t=0,
то ймовірність також дорівнює 0.
t=0,5,
то ймовірність також дорівнює 0,383.
t=1,
то ймовірність також дорівнює 0,683.
t=2,
то ймовірність також дорівнює 0,954.
t=3,
то ймовірність також дорівнює 0,997.
t=4,
то ймовірність також дорівнює 0,999936. і т.д.
Багаторічна практика
свідчить про те, що довірча ймовірність 95,4 % (для t=2) є оптимальною для
більшості розрахунків у різних галузях господарства, тим більше для правових
явищ.
Показники
генеральної сукупності відрізняються від показників вибіркової сукупності на
величину похибки репрезентативності

W –
питома вага одиниць, які мають якусь альтернативну ознаку (частка) в
генеральній сукупності;
w –
питома вага одиниць, які мають якусь альтернативну ознаку (частка) в вибірковій
сукупності.
Наведені формули помилок вибірки дають змогу заздалегідь розрахувати той
обсяг вибірки, при якому відхилення вибіркових показників від генеральних не
перевищать заздалегідь заданих розмірів, що гарантуються з визначеною ймовірністю.