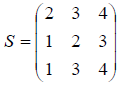Подпространство линейного пространства
1.4 Подпространство линейного пространства
Определение. Подпространством 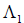 линейного пространства
линейного пространства 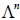 называется множество элементов из
называется множество элементов из 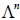 , которое само является пространством, т.е. из
, которое само является пространством, т.е. из
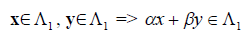
Свойства подпространства линейного пространства 
1. Размерность любого подпространства пространства 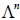 не превосходит n. Очевидно, что само линейное пространство
не превосходит n. Очевидно, что само линейное пространство 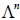 является пространством наибольшей размерности.
является пространством наибольшей размерности.
2. Если 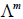 — подпространство линейного пространства
— подпространство линейного пространства 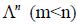 , то любой базис этого подпространства e1,e2,…,em можно дополнить векторами
, то любой базис этого подпространства e1,e2,…,em можно дополнить векторами 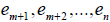 таким образом, что совокупность векторов
таким образом, что совокупность векторов 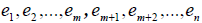 будет являться базисом линейного пространства
будет являться базисом линейного пространства 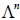 . Линейное подпространство, имеющее своим базисом совокупность векторов e1,e2,…,em, иногда называют линейной оболочкой, натянутой на эти векторы.
. Линейное подпространство, имеющее своим базисом совокупность векторов e1,e2,…,em, иногда называют линейной оболочкой, натянутой на эти векторы.
Задачи.
Задача 1: Будет ли линейным пространством множество всех положительных чисел R+
Решение. Ответ зависит от способа введения операций сложения и умножения на число элементов рассматриваемого множества.
1°. Пусть операции вводятся «естественным” образом. В этом случае множество положительных чисел не образует линейного пространства, поскольку в нем отсутствует нулевой элемент.
2°. Если операцию «сложения” определить как обычное произведение двух чисел, а «умножение на число 1 ” определить как возведение положительного числа в степень 1 , то множество положительных чисел будет являться линейным пространством, в котором роль нулевого элемента играет число «1”.
Задача2: Проверить, что элементы g1,g2,g3 образуют базис в 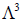 и найти координатное представление элемента x в этом базисе, если в некотором исходном базисе:
и найти координатное представление элемента x в этом базисе, если в некотором исходном базисе:
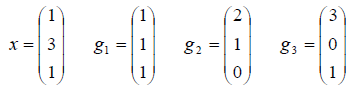
Решение.
1°. Для того чтобы из элементов g1,g2,g3 можно было образовать в 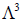 базис, необходимо и достаточно, чтобы эти элементы были линейно независимыми. Данное условие равносильно тому, что определитель матрицы, этих векторов, отличен от нуля и ранг не меньше 3.
базис, необходимо и достаточно, чтобы эти элементы были линейно независимыми. Данное условие равносильно тому, что определитель матрицы, этих векторов, отличен от нуля и ранг не меньше 3.
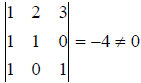 и ранг равен 3
и ранг равен 3
Значит элементы g1,g2,g3 образуют базис в 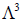
2°. Обозначим искомые координаты элемента x через 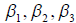 б тогда
б тогда 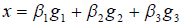 . Запишем в координатной форме:
. Запишем в координатной форме:
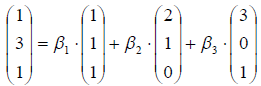
Составим систему:
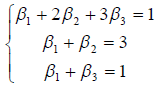 Решив ее методом Гаусса получим:
Решив ее методом Гаусса получим: 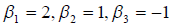
Откуда следует, что элемент x в базисе g1,g2,g3 имеет координатное представление
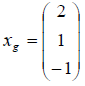
Задача 3: Найти матрицу перехода от базиса в 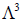 , образованного элементами
, образованного элементами 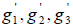 к базису
к базису 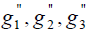 если в некотором исходном базисе:
если в некотором исходном базисе:
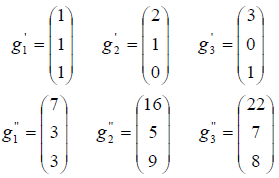
Решение: Пусть x,x’,x» обозначают координатные столбцы элемента x в трех базисах: исходном, 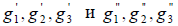 соответственно. Тогда имеют место равенства
соответственно. Тогда имеют место равенства 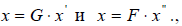 где матрицы G и F составлены из координатных столбцов базисных элементов
где матрицы G и F составлены из координатных столбцов базисных элементов 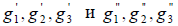 то есть
то есть
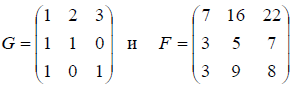
Обозначим через S матрицу перехода от базиса 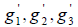 к базису
к базису 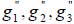 для которой
для которой 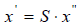 . Но из условий
. Но из условий 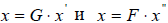 следует, что
следует, что 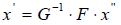
Тогда 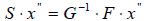 для любого элемента x» , а это означает, что искомая матрица перехода S = G-1 F .
для любого элемента x» , а это означает, что искомая матрица перехода S = G-1 F .
Рассчитав данное произведение получим: