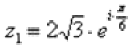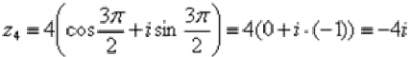Тригонометрическая и показательная форма комплексного числа
Лекция 2. Тригонометрическая и показательная форма комплексного числа
Любое комплексное число (кроме нуля) z = a + bi можно записать в тригонометрической форме: 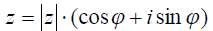 , где z – это модуль комплексного числа, а
, где z – это модуль комплексного числа, а 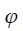 – аргумент комплексного числа
– аргумент комплексного числа
Изобразим на комплексной плоскости число z = a + bi. Для определённости расположим его в первой координатной четверти, т.е. считаем, что a > 0, b > 0:
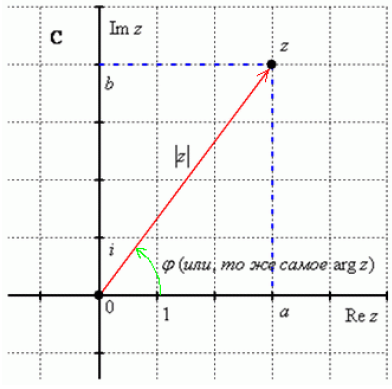
Модулем комплексного числа z называется расстояние от начала координат до соответствующей точки комплексной плоскости. Иначе, модуль – это длина радиус-вектора. Модуль комплексного числа z стандартно обозначают: |z| или r.
По теореме Пифагора легко вывести формулу для нахождения модуля комплексного числа: z = a2 + b2 . Данная формула справедлива для любых значений «а» и «бэ».
Аргументом комплексного числа z называется угол 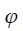 между положительной полуосью действительной оси Re z и радиус-вектором, проведенным из начала координат к соответствующей точке. Аргумент не определён для единственного числа: z = 0 .
между положительной полуосью действительной оси Re z и радиус-вектором, проведенным из начала координат к соответствующей точке. Аргумент не определён для единственного числа: z = 0 .
Аргумент комплексного числа z стандартно обозначают: 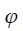 или arg z .
или arg z .
Из геометрических соображений получается следующая формула для нахождения аргумента: 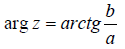 . Внимание! Данная формула работает только в правой полуплоскости! Если комплексное число располагается не в 1-й и не 4-й координатной четверти, то формула будет немного другой.
. Внимание! Данная формула работает только в правой полуплоскости! Если комплексное число располагается не в 1-й и не 4-й координатной четверти, то формула будет немного другой.
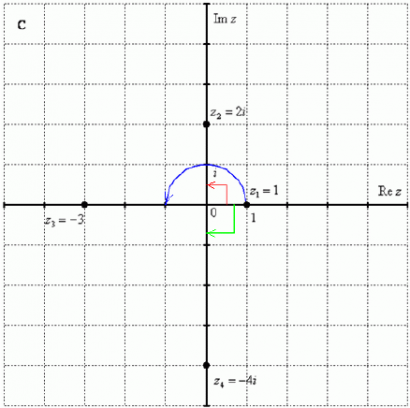
Пример 7: Представить в тригонометрической форме комплексные числа: z1 = 1, z2 = 2i, z3 = -3, z4 = -4i
Выполним чертёж:
1) Представим в тригонометрической форме число 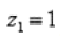 . Найдем его модуль и аргумент.
. Найдем его модуль и аргумент. 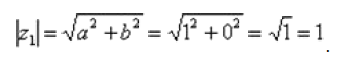
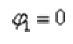 (число лежит непосредственно на действительной положительной полуоси).
(число лежит непосредственно на действительной положительной полуоси).
Таким образом, число в тригонометрической форме: 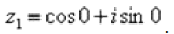
Обратное проверочное действие: 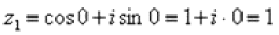
2) Представим в тригонометрической форме число 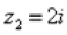 . Найдем его модуль и аргумент.
. Найдем его модуль и аргумент.
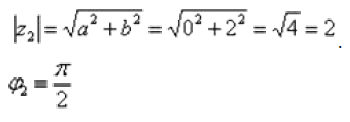
Таким образом, число в тригонометрической форме: 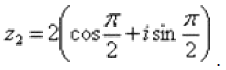
Обратно получим алгебраическую форму числа (заодно выполнив проверку): 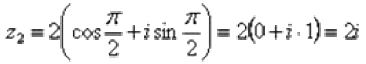
3) Представим в тригонометрической форме число  . Найдем его модуль и аргумент.
. Найдем его модуль и аргумент.
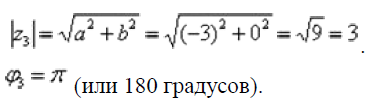
Таким образом, число в тригонометрической форме: 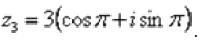
Проверка: 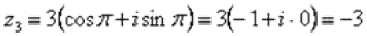
4) Представим в тригонометрической форме число 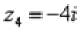 . Найдем его модуль и аргумент.
. Найдем его модуль и аргумент.
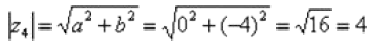
Аргумент можно записать двумя способами:
Первый способ: 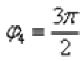 (270 градусов), и, соответственно:
(270 градусов), и, соответственно: 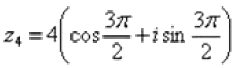 .
.
Второй способ: Если угол больше 180 градусов, то его записывают со знаком минус и противоположной ориентацией («прокруткой») угла: 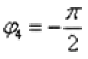 (минус 90 градусов).
(минус 90 градусов).
Легко заметить, что 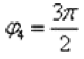 и
и 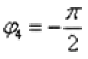 – это один и тот же угол.
– это один и тот же угол.
Таким образом, запись принимает вид: 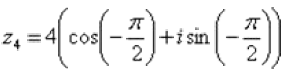
Итак, как уже отмечалось, с модулем проблем не возникает, всегда следует использовать формулу 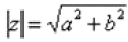 . А вот формулы для нахождения аргумента будут разными, это зависит от того, в какой координатной четверти лежит число
. А вот формулы для нахождения аргумента будут разными, это зависит от того, в какой координатной четверти лежит число 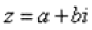 . При этом возможны три варианта:
. При этом возможны три варианта:
1) Если a > 0 (1-ая и 4-ая координатные четверти, или правая полуплоскость), то аргумент нужно находить по формуле 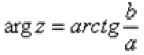 .
.
2) Если a< 0, b > 0 (2-ая координатная четверть), то аргумент нужно находить по формуле 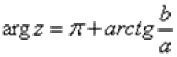 .
.
3) Если a< 0, b< 0 (3-я координатная четверть), то аргумент нужно находить по формуле 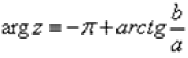 .
.
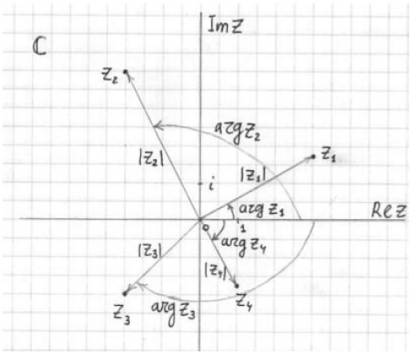
Пример 8 Представить в тригонометрической форме комплексные числа: 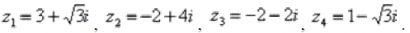
Представим в тригонометрической форме число 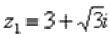 . Найдем его модуль и аргумент.
. Найдем его модуль и аргумент. 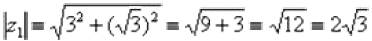 . Поскольку a > 0 (случай 1), то
. Поскольку a > 0 (случай 1), то 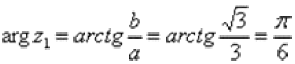 . Таким образом:
. Таким образом: 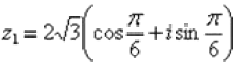 – z1 число в тригонометрической форме.
– z1 число в тригонометрической форме.
Представим в тригонометрической форме число 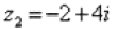 . Найдем его модуль и аргумент.
. Найдем его модуль и аргумент.
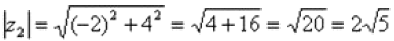
Поскольку a< 0, b > 0 (случай 2), то
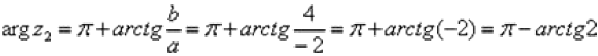
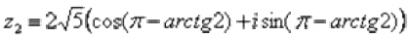 – число z2 в тригонометрической форме.
– число z2 в тригонометрической форме.
Есть простой способ проверки. Если выполнять чертеж на клетчатой бумаге в том масштабе, (1 ед. = 1 см), то можно взять линейку и измерить модуль в сантиметрах. Если есть транспортир, то можно непосредственно по чертежу измерить и угол.
Представим в тригонометрической форме число 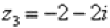 . Найдем его модуль и аргумент.
. Найдем его модуль и аргумент. 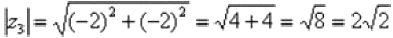 . Поскольку a< 0, b< 0 (случай 3), то
. Поскольку a< 0, b< 0 (случай 3), то 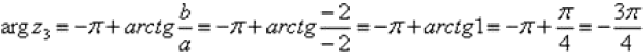 . Таким образом:
. Таким образом: 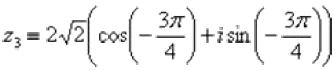 – z3 число в тригонометрической форме.
– z3 число в тригонометрической форме.
Представим в тригонометрической форме число 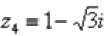 . Найдем его модуль и аргумент.
. Найдем его модуль и аргумент.
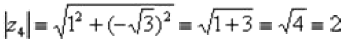
Поскольку a > 0 (случай 1), то 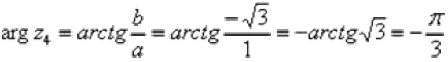 (минус 60 градусов).
(минус 60 градусов).
Таким образом:
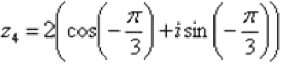 – число z4 в тригонометрической форме.
– число z4 в тригонометрической форме.
Кроме графического метода проверки, существует и проверка аналитическая, которая уже проводилась в Примере 7. Используем таблицу значений тригонометрических функций, при этом учитываем, что угол 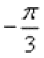 – это в точности табличный угол
– это в точности табличный угол 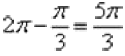 (или 300 градусов):
(или 300 градусов):
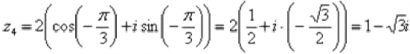 – z4 число в исходной алгебраической форме.
– z4 число в исходной алгебраической форме.
Любое комплексное число (кроме нуля) z = a + bi можно записать в показательной форме: 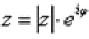 , где |z| – это модуль комплексного числа, а
, где |z| – это модуль комплексного числа, а 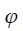 – аргумент комплексного числа.
– аргумент комплексного числа.
Что нужно сделать, чтобы представить комплексное число в показательной форме Почти то же самое: выполнить чертеж, найти модуль и аргумент. И записать число в виде 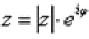 .
.
Например, для числа 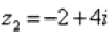 предыдущего примера у нас найден модуль и аргумент:
предыдущего примера у нас найден модуль и аргумент: 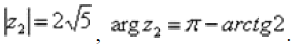 Тогда данное число в показательной форме запишется следующим образом:
Тогда данное число в показательной форме запишется следующим образом: 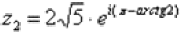 .
.
Число 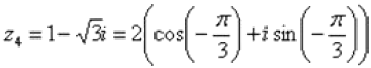 в показательной форме будет выглядеть так:
в показательной форме будет выглядеть так: 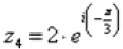
Число 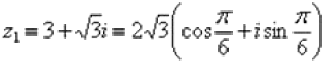 – так:
– так: