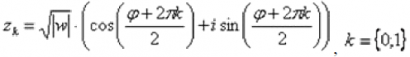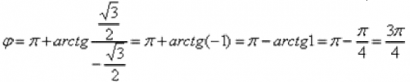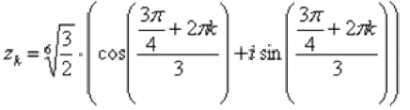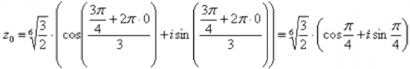Возведение комплексных чисел в степень
Содержание страницы:
Лекция 3. Возведение комплексных чисел в степень
Начнем с квадрата.
Пример 9 Возвести в квадрат комплексное число 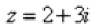
Здесь можно пойти двумя путями, первый способ это переписать степень как произведение множителей 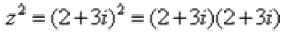 и перемножить числа по правилу умножения многочленов.
и перемножить числа по правилу умножения многочленов.
Второй способ состоит в применение известной школьной формулы сокращенного умножения 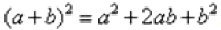 :
:
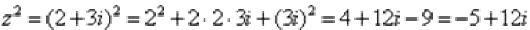
Для комплексного числа легко вывести свою формулу сокращенного умножения: 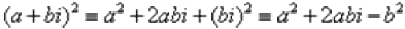 . Аналогичную формулу можно вывести для квадрата разности, а также для куба сумма и куба разности.
. Аналогичную формулу можно вывести для квадрата разности, а также для куба сумма и куба разности.
Что делать, если комплексное число нужно возвести, скажем, в 5-ую, 10-ую или 100-ую степень Ясно, что в алгебраической форме проделать такой трюк практически невозможно.
И здесь на помощь приходит тригонометрическая форма комплексного числа и, так называемая, формула Муавра: Если комплексное число представлено в тригонометрической форме 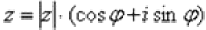 , то при его возведении в натуральную степень
, то при его возведении в натуральную степень 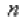 справедлива формула:
справедлива формула:
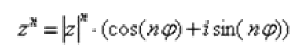
Данная формула следует из правила умножения комплексных чисел, представленных в тригонометрической форме: чтобы найти произведение чисел 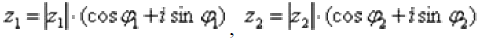 , нужно перемножить их модули и сложить аргументы:
, нужно перемножить их модули и сложить аргументы:
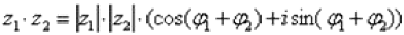
Аналогично для показательной формы: если 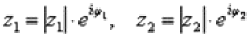 , то:
, то: 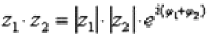
Пример 10 Дано комплексное число 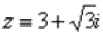 , найти z20.
, найти z20.
Сначала нужно представить данное число в тригонометрической форме. В примере 8 мы это уже сделали: 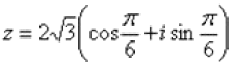
Тогда, по формуле Муавра:
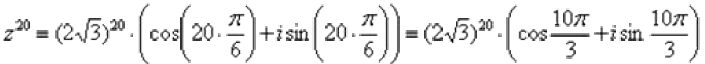
Упаси боже, не нужно считать на калькуляторе 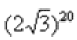 , а вот угол в большинстве случае следует упростить. Как упростить Образно говоря, нужно избавиться от лишних оборотов. Один оборот составляет радиан
, а вот угол в большинстве случае следует упростить. Как упростить Образно говоря, нужно избавиться от лишних оборотов. Один оборот составляет радиан 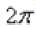 или 360 градусов. Выясним сколько у нас оборотов в аргументе
или 360 градусов. Выясним сколько у нас оборотов в аргументе 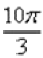 . Для удобства делаем дробь правильной:
. Для удобства делаем дробь правильной: 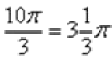 , после чего становится хорошо видно, что можно убавить один оборот: Таким образом, окончательный ответ запишется так:
, после чего становится хорошо видно, что можно убавить один оборот: Таким образом, окончательный ответ запишется так:
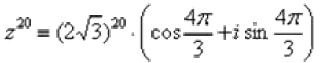
Пример 11 Дано комплексное число 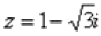 , найти z30. Полученный аргумент (угол) упростить, результат представить в алгебраической форме.
, найти z30. Полученный аргумент (угол) упростить, результат представить в алгебраической форме.
Представим число в тригонометрической форме: 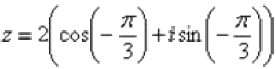 (это число z4 Примера 8). Используем формулу Муавра
(это число z4 Примера 8). Используем формулу Муавра 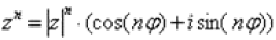 :
:
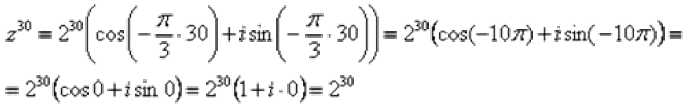
Отдельная разновидность задачи возведения в степень – это возведение в степень чисто мнимых чисел.
Пример 12 Возвести в степень комплексные числа i10, i33, (-i)21. Здесь тоже всё просто, главное, помнить знаменитое равенство. Если мнимая единица возводится в четную степень, то техника решения такова: 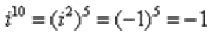
Если мнимая единица возводится в нечетную степень, то «отщипываем» одно «и», получая четную степень: 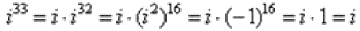
Если есть минус (или любой действительный коэффициент), то его необходимо предварительно отделить:
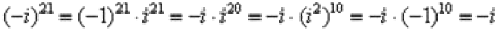
Пример 13 Возвести в степень комплексные числа 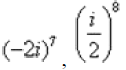
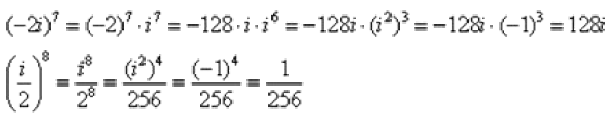
Извлечение корней из комплексных чисел.
Квадратное уравнение с комплексными корнями
Рассмотрим пример: 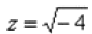
Нельзя извлечь корень Если речь идет о действительных числах, то действительно нельзя. В комплексных числах извлечь корень – можно! А точнее, два корня:
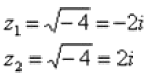
Действительно ли найденные корни являются решением уравнения 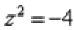
Выполним проверку: 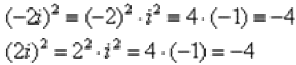
Что и требовалось проверить.
Часто используется сокращенная запись, оба корня записывают в одну строчку под «одной гребёнкой»: 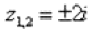 .
.
Такие корни также называют сопряженными комплексными корнями.
Как извлекать квадратные корни из отрицательных чисел, думаю, всем понятно: 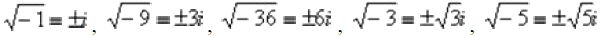 и т.д. Во всех случаях получается двасопряженных комплексных корня.
и т.д. Во всех случаях получается двасопряженных комплексных корня.
Пример 14 Решить квадратное уравнение 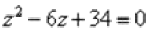
Вычислим дискриминант: 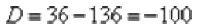
Дискриминант отрицателен, и в действительных числах уравнение решения не имеет. Но корень можно извлечь в комплексных числах!
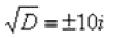
По известным формулам получаем два корня:
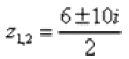
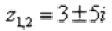 – сопряженные комплексные корни
– сопряженные комплексные корни
Таким образом, уравнение 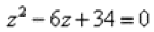 имеет два сопряженных комплексных корня:
имеет два сопряженных комплексных корня: 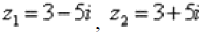
Нетрудно понять, что в поле комплексных чисел «школьное» квадратное уравнение всегда при двух корнях! И вообще, любое уравнение вида 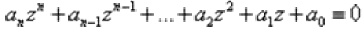 имеет ровно n корней, часть из которых могут быть комплексные
имеет ровно n корней, часть из которых могут быть комплексные
Пример 15 Найти корни уравнения 4z2+1=0 и разложить квадратный двучлен на множители.
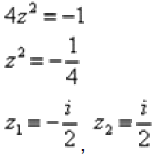
Разложим квадратный двучлен на множители:
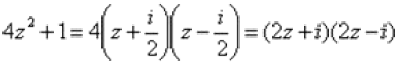
Как извлечь корень из произвольного комплексного числа
Уравнение вида 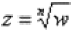 имеет ровно n корней
имеет ровно n корней 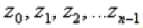 , которые можно найти по формуле:
, которые можно найти по формуле:
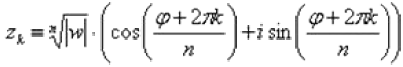
где 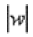 – это модуль комплексного числа
– это модуль комплексного числа 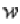 ,
, 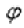 – его аргумент, а параметр принимает значения:
– его аргумент, а параметр принимает значения: 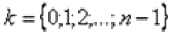
Пример 16 Найти корни уравнения 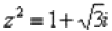
Перепишем уравнение в виде 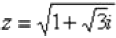
В данном примере 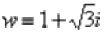 , n=2 , поэтому уравнение будет иметь два корня: z0 и z1 .
, n=2 , поэтому уравнение будет иметь два корня: z0 и z1 .
Общую формулу можно сразу детализировать:
Теперь нужно найти модуль и аргумент комплексного числа 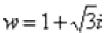 :
:
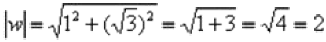
Число 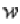 располагается в первой четверти, поэтому:
располагается в первой четверти, поэтому:
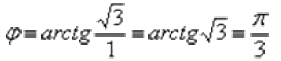
Еще более детализируем формулу:
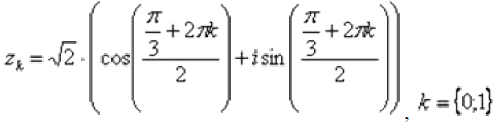
Подставляя в формулу значение k=0, получаем первый корень:
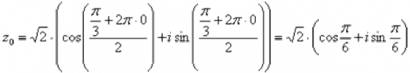
Подставляя в формулу значение k=1, получаем второй корень:
Ответ: 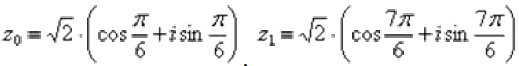
Пример 17 Найти корни уравнения 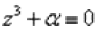 , где
, где 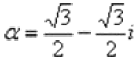
Сначала представим уравнение в виде 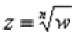 :
:

Если 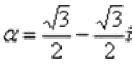 , тогда
, тогда 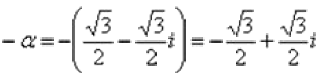
Обозначим 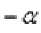 привычной формульной буквой:
привычной формульной буквой: 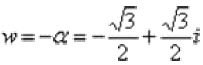
Таким образом, требуется найти корни уравнения 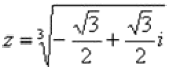
В данном примере n=3, а значит, уравнение имеет ровно три корня: z0, z1, z2
Детализирую общую формулу: 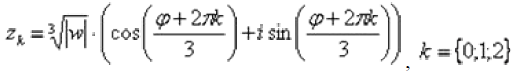
Найдем модуль и аргумент комплексного числа 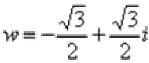 :
:
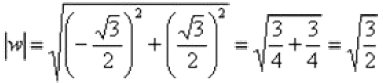
Число 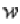 располагается во второй четверти, поэтому:
располагается во второй четверти, поэтому:
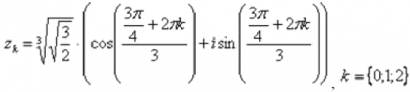
Еще раз детализирую формулу:
Корень удобно сразу же упростить:
Подставляем в формулу значение k=0 и получаем первый корень:
Подставляем в формулу значение k=2 и получаем третий корень:
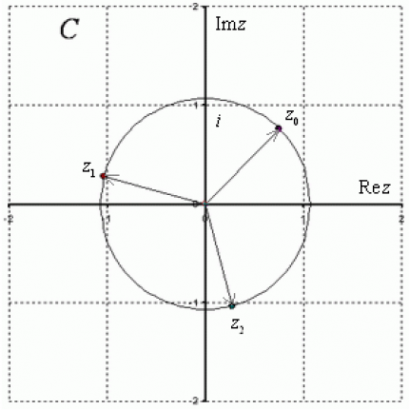
Очень часто полученные корни требуется изобразить геометрически:
Как выполнить чертеж
Сначала на калькуляторе находим, чему равен модуль корней 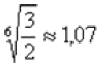 и чертим циркулем окружность данного радиуса. Все корни будут располагаться на данной окружности.
и чертим циркулем окружность данного радиуса. Все корни будут располагаться на данной окружности.
Теперь берем аргумент первого корня 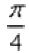 и выясняем, чему равняется угол в градусах:
и выясняем, чему равняется угол в градусах: 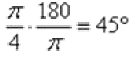 . Отмеряем транспортиром
. Отмеряем транспортиром 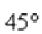 и ставим на чертеже точку z0.
и ставим на чертеже точку z0.
Берем аргумент второго корня 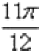 и переводим его в градусы:
и переводим его в градусы: 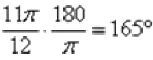 .
.
Отмеряем транспортиром 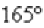 и ставим на чертеже точку z1.
и ставим на чертеже точку z1.
По такому же алгоритму строится точка z2.