Лекция 5.
Евклидово пространство En

Определение евклидова пространства

Определение 1. Вещественное линейное пространство называется евклидовым, если в нём определена операция, ставящая в соответствие любым двум векторам x и y из этого пространства число, называемое скалярным произведением векторов x и y и обозначаемое (x,y) , для которого выполнены условия:

1. (x,y) = (y,x);

2. (x + y,z) = (x,z) + (y,z) , где z - любой вектор, принадлежащий данному линейному пространству;

3. (?x,y) = ? (x,y) , где ? - любое число;

4. (x,x) ? 0 , причём (x,x) = 0 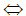 x = 0.

Например, в линейном пространстве одностолбцовых матриц скалярное произведение векторов

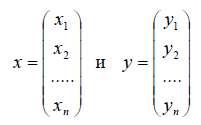
можно определить формулой

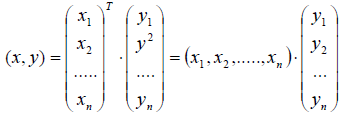
Евклидово пространство размерности n обозначают En. Заметим, что существуют как конечномерные, так и бесконечномерные евклидовы пространства.

Определение 2. Длиной (модулем) вектора x в евклидовом пространстве En называют (x,x) и обозначают её так: |x| = (x,x) . У всякого вектора евклидова пространства существует длина, причём у нулевого вектора она равна нулю.

Умножая ненулевой вектор x на число 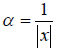 , мы получим вектор  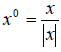, длина которого равна единице. Эта операция называется нормированием вектора x.

Например, в пространстве одностолбцовых матриц длину вектора 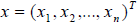 можно определить формулой: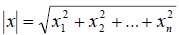 

Неравенство Коши-Буняковского

Пусть x? En и y ? En – любые два вектора. Докажем, что для них имеет место неравенство:

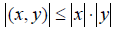(Неравенство Коши-Буняковского)

Доказательство. Пусть ? - любое вещественное число. Очевидно, что (?x ? y,?x ? y) ? 0. С другой стороны, в силу свойств скалярного произведения можем написать

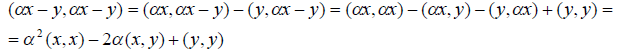
Получили, что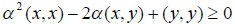 

Дискриминант этого квадратного трёхчлена не может быть положительным, т.е. 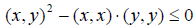 , откуда вытекает: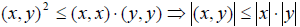 

Неравенство доказано.

Неравенство треугольника

Пусть x и y - произвольные векторы евклидова пространства En , т.е. x? En и y ? En. 

Докажем, что 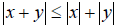 . (Неравенство треугольника).

Доказательство. Очевидно, что 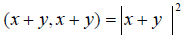 С другой стороны,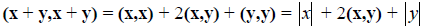. Принимая во внимание неравенство Коши-Буняковского, получим

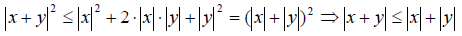
Неравенство треугольника доказано. 

Норма евклидова пространства

Определение 1. Линейное пространство ? называется метрическим, если любым двум элементам этого пространства x и y поставлено в соответствие неотрицательное число ? (x,y) , называемое расстоянием между x и y , (? (x,y) ? 0) , причём выполняются условия (аксиомы):

1) ? (x,y) = 0  x = y

2) ? (x,y) = ? (y,x) (симметрия);

3) для любых трёх векторов x, y и z этого пространства ? (x,y) ? ? (x,z) + ? (z,y).

Замечание. Элементы метрического пространства обычно называют точками.

Евклидово пространство En – метрическое, причём в качестве расстояния между векторами x? En и y? En можно взять x ? y.

Так, например, в пространстве одностолбцовых матриц, где

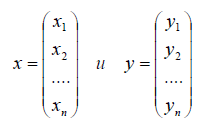
получим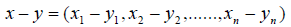 

следовательно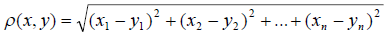 

Определение 2. Линейное пространство ? называется нормированным, если каждому вектору x из этого пространства поставлено в соответствие неотрицательное число, называемое его нормой x. При этом выполняются аксиомы:

1) 

 

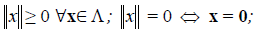
2) 

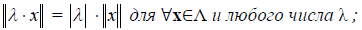
3) 

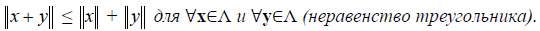
Нетрудно видеть, что нормированное пространство является метрическим пространством. В самом деле, в качестве расстояния между x и y можно взять 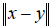 . В евклидовом пространстве En в качестве нормы любого вектора x? En принимается его длина, т.е.  .

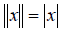Итак, евклидово пространство En является метрическим пространством и более того, евклидово пространство En является нормированным пространством.

Угол между векторами

Определение 1. Углом между ненулевыми векторами a и b евклидова пространства En называют число 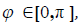 для которого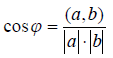 

Определение 2. Векторы x и y евклидова пространства En называются ортогональными, если для них выполняется равенство (x,y) = 0.

Если x и y - ненулевые, то из определения следует, что угол между ними равен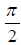 

Заметим, что нулевой вектор по определению считается ортогональным любому вектору.

Пример. В геометрическом (координатном) пространстве ?3, которое является частным случаем евклидова пространства, орты i, j и k взаимно-ортогональны.

Ортонормированный базис

Определение 1. Базис e1,e2,...,en евклидова пространства En называется ортогональным, если векторы этого базиса попарно ортогональны, т.е. если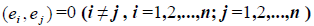

Определение 2. Если все векторы ортогонального базиса e1, e2,...,en единичны, т.е. ei = 1 (i = 1,2,...,n ) , то базис называется ортонормированным, т.е. для ортонормированного базиса

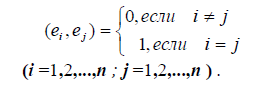
Теорема. (о построении ортонормированного базиса)

Во всяком евклидовом пространстве E n существуют ортонормированные базисы.

Доказательство. Докажем теорему для случая n = 3. 

Пусть E1,E2,E3 - некоторый произвольный базис евклидова пространства E3 Построим какой-нибудь ортонормированный базис 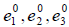 в этом пространстве. Положим  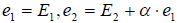, где ? - некоторое вещественное число, которое выберем таким образом, чтобы было (e1,e2) = 0, тогда получим

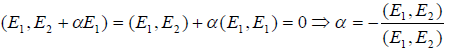
причём очевидно, что ? = 0 , если E1 и E2 ортогональны, т.е. в этом случае e2 = E2 , а 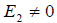, т.к. это базисный вектор.

Далее, определим вектор e3 равенством 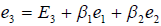 , причём числа  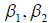определяется из условия ортогональности вектора e3 с векторами e1,e2, т.е.

 

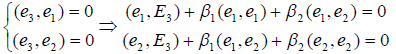
Учитывая, что (e1,e2) = 0, получим

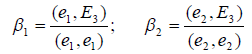
Очевидно, что 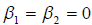, если e1 и e2 ортогональны с вектором E3, т.е. в этом случае следует взять e3 = E3. Вектор E3 ? 0 , т.к. E1, E2 и E3 линейно независимы, следовательно e3 ? 0.

Кроме того, из приведённого рассуждения следует, что e3 нельзя представить в виде линейной комбинации векторов e1 и e2 , следовательно векторы e1, e2, e3 линейно независимы и попарно ортогональны, следовательно, их можно взять в качестве базиса евклидова пространства E3. Остаётся только пронормировать построенный базис, для чего достаточно каждый из построенных векторов разделить на его длину. Тогда получим

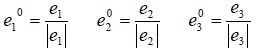
Итак, мы построили базис 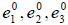 - ортонормированный базис. Теорема доказана.

Применённый способ построения ортонормированного базиса из произвольного базиса называется процессом ортогонализации. Заметим, что в процессе доказательства теоремы мы установили, что попарно ортогональные векторы линейно независимы. Кроме того, если 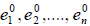 - ортонормированный базис в En, тогда для любого вектора x? En имеет место единственное разложение

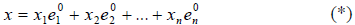
где x1, x2,..., xn - координаты вектора x в этом ортонормированном базисе. 

Так как

 

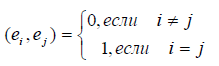то умножив скалярно равенство (*) на  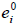, получим  .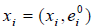

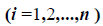В дальнейшем мы будем рассматривать только ортонормированные базисы, а потому для простоты их записи нолики сверху у базисных векторов 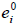 мы будем опускать.

Повернутися назад