Базис линейного пространства и координаты вектора. Размерность линейного пространства

1.3. Базис линейного пространства и координаты вектора. Размерность линейного пространства

Пусть векторы (элементы) a1 , a2 ,…,an принадлежат линейному пространству и пусть c1 ,c2 ,…,cn — какие-то произвольные числа. Выражение c1 a1 + c2 a2 + …+ cn an называется линейной комбинацией векторов (элементов) a1 , a2 ,…,an , а числа c1 ,c2 ,…,cn — коэффициентами этой линейной комбинации.

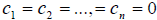Определение 1. Векторы (элементы) a1 , a2 ,…,an называются линейно зависимыми, если   при условии, что не все коэффициенты этой линейной комбинации равны нулю; если же соотношение (1) выполняется лишь при условии, что , то векторы называются линейно независимыми.

Нетрудно показать, что если векторы 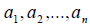 линейно зависимы, то хотя бы один из них можно представить в виде линейной комбинации остальных и наоборот; кроме того, если векторы  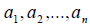линейно независимы, то ни один из них нельзя представить в виде линейной комбинации остальных и наоборот.

Определение 2. Любая совокупность n линейно независимых векторов 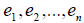 линейного пространства называется базисом этого пространства, если всякий вектор x можно представить в виде линейной комбинации векторов  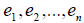т.е.

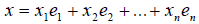
Такое представление вектора x называется разложением его по данному базису. Числа x1 , x2 , x3 ,…, xn, которые являются коэффициентами в разложении вектора по данному базису, называются координатами вектора в этом базисе и записываются так: x = (x1, x2,…,xn) или так [x1, x2,…,xn ], или в виде матрицы-столбца: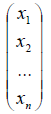 

Теорема. Координаты вектора x относительно некоторого базиса e1,e2 ,…,en этого линейного пространства определяются единственным образом.

Доказательство. Пусть имеет место такое разложение вектора x относительно некоторого базиса этого линейного пространства:

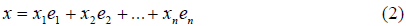
и пусть имеет место другое разложение этого же вектора относительно это-го же базиса:

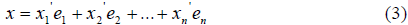
Вычитая почленно (3) из (2), получим:

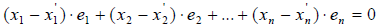
Так как базисные векторы e1 ,e2 ,…,en линейно независимы, то это значит, что коэффициенты линейной комбинации могут быть только нулями, значит 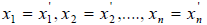 Теорема доказана.

В качестве примера рассмотрим пространство многочленов Pn(x) степени n . В качестве базиса можно взять одночлены 1, x, x2 , x3 ,…, xn . Они линейно независимы, и любой многочлен Pn(x) можно представить в виде:

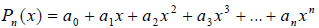
В силу определения коэффициенты a0 ,a1 , a2 ,…,an являются координатами многочлена Pn(x) в выбранном базисе, т.е. можно записать: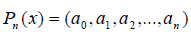 

Можно доказать, что если линейное пространство имеет базис, то он не единственный. Однако же различные базисы данного линейного пространства состоят из одного и того же числа n векторов, которое и определяет размерность линейного пространства.

Определение 3. Говорят, что линейное пространство имеет размерность равную n , если n — число базисных векторов, пространство при этом обозначают n.

Пусть в n даны два базиса: «старый”- 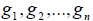  и «новый”-  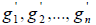 с соответствующими координатными разложениями элемента x :  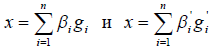Пусть, кроме того, известны разложения элементов «нового” базиса по элементам «старого”: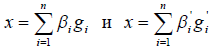 

Определение 4: Матрица 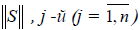 столбец которой состоит из коэффициентов  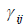координатных разложений элементов «нового” базиса по элементам «старого”, называется матрицей перехода от базиса  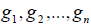к базису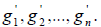 

Определение 5: Координаты 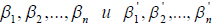 связаны соотношениями 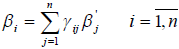, называемыми формулами перехода, где коэффициенты  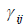– элементы матрицы перехода S.

Элементы конечномерного линейного пространства могут представляться матрицами (столбцами) и правила выполнения операций с этими элементами совпадают с определением соответствующих матричных операций.

Если 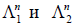 — два линейных пространства (оба вещественных или оба комплексных) и если  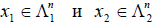, то между ними можно установить взаимно однозначное соответствие, точно так же как и между произведениями ax1 и ax2 и суммами x1 + y1 и x2 + y2 , где  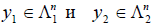. Такое свойство линейных пространств называется изоморфизмом, а сами линейные пространства называются изоморфными.

Определение 6. Два линейных пространства 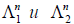 называются изоморфными, если существует взаимно однозначное отображение  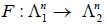такое, что для  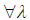и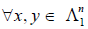 

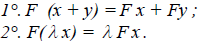
Отображение F называется изоморфизмом линейных пространств .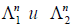

Теорема: Максимальное число линейно независимых элементов в любом конечном наборе элементов из 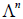 равно рангу матрицы, столбцы которой содержат координаты элементов данного набора в некотором базисе.

Следствие 1: k элементов в 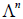 линейно зависимы тогда и только тогда, когда ранг матрицы, столбцы которой содержат координаты этих элементов в некотором базисе, меньше, чем min{n, k} .

Следствие 2: Матрица перехода невырожденная, то есть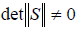 

В заключение заметим, что если базис состоит из конечного числа элементов, то такое линейное пространство называется конечномерным, если же существует бесконечно много линейно независимых векторов, то такое линейное пространство называется безконечномерным. Примером бесконечномерного пространства может служить пространство всевозможных функций, непрерывных на данном промежутке, линейные операции в котором определяются обычным образом.