ТЕМА 7. Умовивід як складна форма мислення
Зміст сторінки:
ТЕМА 7. Умовивід як складна форма
мислення
1. Сутність, структура та види умовиводів
2.1. Безпосередні дедуктивні умовиводи
2.2. Опосередковані дедуктивні умовиводи
1. Сутність,
структура та види умовиводів
Сьогодні ми приступаємо до вивчення останньої з основних
логічних форм. Можливо, вивчення попередніх форм мислення здалося вам справою дещо абстрактною та
відірваною від життя. Пов’язане це з тим, що, вивчаючи поняття та судження, ми наше мислення
штучно дробили на складові частини. Але це було необхідно для того, щоб
підготуватися до засвоєння найскладнішої логічної форми – умовиводу.
Саме у формі умовиводів ми й мислимо. Умовиводи
пов’язані з вивідними знаннями – тобто знаннями, виведеними з тих, що вже є. Ще
ці знання називаються опосередкованими – на відміну від безпосередніх,
отриманних за допомогою органів почуттів. Логічною формою отримання вивідних
знань є умовивід.
Умовивід – це форма мислення, в якій з одного або
кількох суджень виводиться нове судження, що містить нове знання.
Термін “умовивід” застосовується у подвійному значенні.
Під умовиводом розуміють:
1) процес виведення нового знання з суджень;
2) саме нове судження як результат логічної операції.
Будь-який умовивід складається із засновків та висновку.
Засновки – це судження, з
яких виводиться нове знання.
Висновок – судження,
виведене із засновків.
Наприклад, візьмемо умовивід: “Береза – дерево. Дерево –
рослина. Отже, береза – рослина”. У цьому умовиводі перші два судження є
засновками, а третє, що стоїть після слова “отже” – висновок.
Зрозуміло, що нове знання не можна вивести з поєднання
будь-яких суджень. Для умовиводу необхідно, щоб між засновками був логічний зв’язок. Наприклад, із таких
двох суджень, як “Усі дерева – рослини” та “Залізо –метал” не можна зробити
ніякого висновку, тому, що ці судження відображають об’єкти різних предметних
областей, ніяк логічно не пов’язані. Отже, поєднання цих суджень не є умовиводом.
У будь-якому умовиводі необхідно розрізняти три види
знань:
1) вихідне знання – те, з якого виводиться нове
знання – міститься у засновках умовиводу;
2) вивідне знання – міститься у висновку;
3) обгрунтовуюче знання – знання, що пояснює
правомірність висновку із засновків. Саме це знання не міститься у судженнях,
що входять до складу умовиводів, але без нього правильного умовиводу зробити не
можна. Воно міститься в аксіомах та правилах умовиводів і складає логічну основу висновків, тобто
чому саме такий висновок з цих суджень правомірний та невідворотній.
За ступенем загальності засновків та висновку умовиводи
поділяються на три групи:
1) дедуктивні, коли думка йде від більш загальних
знань до менш загальних;
2) індуктивні, коли думка розвивається від менш
загальних знань до більш загальних;
3) традуктивні (за аналогією), коли засновки і
висновок виражаютиь знання однакового ступеню загальності.
2. Дедуктивні
умовиводи
Приклад дедуктивного умовиводу:
Усі підприємства країни повинні вести бухгалтерський облік згідно з
установленими правилами.
ТОВ “Ромашка” – підприємство цієї
країни.
______________________________________
Отже, ТОВ “Ромашка” повинне вести бухгалтерський облік згідно з
установленими правилами.
Тут висновок іде від знання про цілий клас – усі
підприємства, до знання про окремого представника цього класу – ТОВ “Ромашка”.
При цьому у дедуктивних умовиводах при переході від загального до часткового
висновок завжди єдино можливий, обов’язковий та невідворотній.
Дедуктивні умовиводи у
першу чергу поділяються на безпосередні та опосередковані.
Безпосереднім називається такий дедуктивний
умовивід, у якому висновок робиться з одного засновку.
Опосередкованим називається такий дедуктивний
умовивід, у якому висновок робиться з двох засновків.
2.1.
Безпосередні ддедуктивні умовиводи
В основному у безпосередніх умовиводах використовуються
правила логічного квадрата та закони логіки.
1. Умовиводи за логічним квадратом.
1.1. Умовивід від підпорядковуючого до підпорядкованого
(від істинності А до істинності І та від істинності Е до істинності О). “Усі
люди смертні” – “Отже, й деякі люди смертні”. “Жоден кит не дихає зябрами” –
“Отже, й деякі кити не дихають зябрами”.
1.2. Умовивід від підпорядкованого до підпорядковуючого
(від хибності І до хибності А та від хибності О до хибності Е). Тут також
очевидно. Якщо хибне часткове ствердження (наприклад, “Деякі кити дихають
жабрами”), то хибне й загальне (“Усі кити дихають жабрами”).
1.3. Умовивід від суперечності (від хибності А до
істинності О, від хибності Е до істинності І, від істинності А до хибності О,
від істинності Е до хибності І та навпаки). Наприклад, якщо істинне А – “Усі
народи мають право на самовизначення”, то хибне частковозаперечне (О) – “Деякі
народи не мають права на самовизначення”. Якщо ж істинне І – “Деякі народи мають
право на самовизначення”, то хибне Е – “Жоден народ не має права на
самовизначення”.
1.4. Умовивід від протилежності (від істинності А до
хибності Е та від істинності Е до хибності А, але не навпаки). Наприклад, з
істинності загальноствердного судження (А) – “Усі народи мають право на
самовизначення” випливає хибність загальнозаперечного (Е) – “Жоден народ не має
права на самовизначення”. Але з хибності А, наприклад, “Усі птахи узимку
улітають на південь”, не випливає істинність Е – “Жоден птах узимку не улітає
на південь”.
1.5. Умовивід від часткової сумісності: з хибності І
випливає істинність О, а з хибності О випливає істинність І, але не навпаки.
Наприклад, з хибності судження О – “Деякі лікарі не мають медичної освіти”
випливає істинне судження О – “Деякі лікарі мають медичну освіту”. Тобто,
принаймні деякі, хоча насправді усі. Але з істинного І (наприклад, “Деякі
студенти опитані”) не випливає ні істинність, ні хибність судження О (“Деякі
студенти не опитані”), яке може бути як істинним, так і хибним.
2. Умовивід за допомогою перетворень. При цьому
ствердне судження перетворюється на заперечне і навпаки.
2.1 Перетворення А на Е: “Усі метали – елементи” –
“Отже, жоден метал не є не елемент”.
2.2. Перетворення Е на А: “Жодна людина не буває
безсмертною” – “Отже, усі люди смертні”.
Аналогічно здійснюються
2.3. Перетворення І на О.
2.4. Перетворення О на І.
Слід пам’ятати, що перетворення заперечних суджень можливе лише тоді, коли вони
містять подвійне заперечення – тоді при перетворенні їх на ствердні воно
відкидається.
3. Умовивід за допомогою обернення. При оберненні
суб’єкт і предикат міняються місцями.
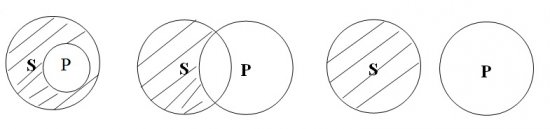
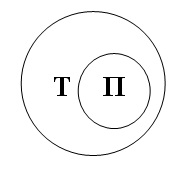
3.1. Судження А обертається на І. «Усі птахи –
тварини» – «Деякі тварини – птахи». Тут це очевидно: «тварини» – більше коло,
птахи – менше:
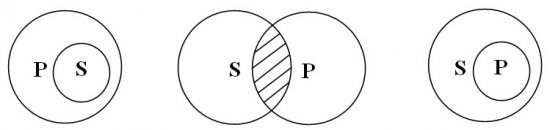
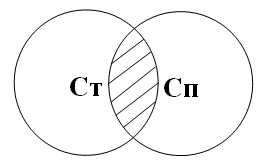
3.2. Судження І обертається,
залишаючися самим собою. “Деякі студенти – спортсмени. Отже, деякі спортсмени –
студенти”:
Тут одночасно і “деякі студенти – спортсмени, і “деякі
спортсмени – студенти”.
3.3. Судження Е також обертається чисто. Це елементарно: “Жоден
крокодил не птах. Отже, жоден птах не крокодил”. Два неспівпадаючих кола:
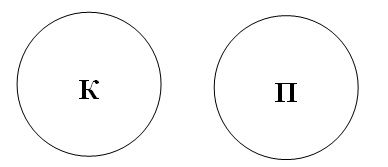
Судження О – не обертається. Візьмемо у загальному
вигляді частковозаперечне судження – “Деякі “S не є Р”. Якщо його
обернути, вийде невизначеність, оскільки можливі 3 варіанти: “Усі Р є S”,
“Деякі Р є S” і “Жодне Р не є S”:
4. Умовивід за допомогою протиставлень.
При протиставленні підмет та присудок міняються місцями, а саме судження зі
ствердного стає заперечним, або із заперечного – ствердним.
Загальна схема протиставлень:
4.1. З А в Е
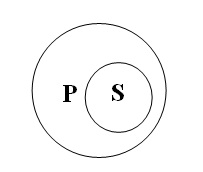
“Усі S є Р” –
“Отже, жодне не Р не є S” (“Усі поети вразливі” – “Жодна невразлива людина не є поетом”).
4.2. З Е в І
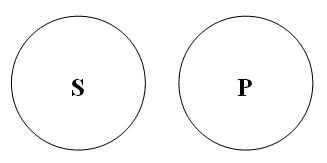
“Жодне S не є Р” – “Отже, деякі не Р є S” (“Жоден поет
не є невразливим” – “Отже, деякі вразливі люди є поетами”).
4.3. З О в І
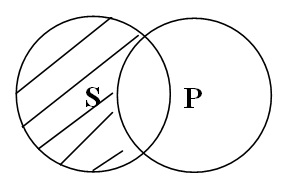
“Деякі S не є Р” – “Отже, деякі не Р є S” (“Деякі
студенти не відмінники” – “Отже, деякі не відмінники є студентами”).
4.4. І – не протиставляється.
“Деякі S є Р”:
Можуть бути різні варіанти. Невизначеність.
2.2. Опосередковані дедуктивні умовиводи (силогізми)
Силогізм – це така форма
дедуктивного умовиводу, в якій із двох суджень
випливає третє, причому одне з двох суджень є загальноствердним або
загальнозаперечним.
У залежності від того, з
якиз видів суджень складається дедуктивний умовивід, дедуктивні силогізми
поділяються на кілька видів. Найбільше значення має (оскільки найчастіше
зустрічається) категоричний силогізм.
Категоричним силогізмомназивається такий дедуктивний умовивід, у якому обидва засновки є категоричними
судженнями.
![]() Категоричний силогізм
Категоричний силогізм
складається з трьох частин – двох засновків і висновку. Засновки та висновок, у
свою чергу, складаються з понять. Поняття, що входять до силогізму, називаються
термінами. Підмет висновку називається меншим терміном, присудок – більшим
терміном, а поняття, яке не входить до висновку, – середнім терміном.
Наприклад:
М – серед. термін Р
Усі метали проводять електрику.
S М
Залізо – метал.
_____________________________
S – менш. Р – більший термін
термін
Залізо проводить електрику.
Або в загальному вигляді для будь-яких S, Р і
М буде істинним:
Усі М є Р.
Усі S є М.
Усі S є Р.
Засновок, до якого входить більший термін, називається
більшим засновком, а засновок, до якого входить менший термін – меншим.
Середній термін входить до обох засновків, пов’язує більший з меншим і зникає у
висновку.
Для того, щоб перевірити, чи правильно складений
силогізм, застосовуються аксіома силогізму, загальні правили та правила фігур
категоричного силогізму.
Аксіома силогізму, з якої випливають усі його правила:
усе, що стверджується стосовно цілого класу, стверджується і стосовно кожної
речі, що входить до нього, і все, заперечуване стосовно цілого класу,
заперечується і стосовно всього, що входить до нього.
Загальні правила силогізму
1. У будь-якому силогізмі повинно бути не менше і не
більше, ніж три терміни.
Коса росте на голові у дівчини.
Це знаряддя – коса.
________________________________
Це знаряддя росте на голові у дівчини.
Тут через порушення одного із законів логіки – закону
тотожності – закрався четвертий термін – коса, але інша. Тому висновок виявився
неправильним.
2. Середній термін повинен бути взятий принаймні в
одному засновку в повному обсязі.
Собака – друг людини.
Ти – мій друг.
_____________________
Ти – собака.
Тут середній термін (друг) узятий не в повному обсязі.
Насправді ж можна бути другом і не бути собакою.
3. Терміни, не взяті у засновках у повному обсязі, не
можуть бути взяті й у висновку в повному обсязі. Приклад порушення цього правила:
Усі злочинці заслуговують покарання.
Деякі англійці – злочинці.
_______________________________
Усі англійці заслуговують покарання.
4. З двох заперечних суджень не можна зробити
умовиводу.
5. Якщо один із засновків заперечний, то й висновок
повинен бути заперечним.
6. З двох часткових суджень не можна зробити
умовиводу.
7. Якщо один із засновків частковий, то й висновок
повинен бути частковим.
Фігури категоричного силогізму
У залежності від місцезнаходження середнього терміна силогізм
може набувати 4 форм, які називають фігурами.
І. М – Р. Менший
засновок завжди ствердний, а більший – загаль-
S – М. ний. Застосовується, коли треба показати
застосування
S – Р. загальних положень до часткових
випадків. Цей силогізм називається юридичним, оскільки за ним будуються вироки:
За це діяння передбачено 5 років ув’язнення.
Н. вчинив це діяння.
_______________________________________
Н. карається 5-річним ув’язненням.
ІІ. Р – М. У цій
фігурі один із засновків повинен бути запереч-
S – М.ним, а більший – загальним. За допомогою цієї
фігу-
S – Р. ри відкидаються хибні
положення. Наприклад:
Для того, щоб учинити злочин, необхідно бути на місці
злочину в момент його вчинення.
Підозрюваний у момент
вчинення злочину не був на місці злочину.
__________________________________________________________
Підозрюваний не вчинив злочин.
ІІІ. М – Р. Менший засновок завжди стверджувальний, а висно-М – S. вок – частковий. Часто тут позначаютьсявиключен-
S – Р. ня з правил. Наприклад:
Ртуть не тверда.
Ртуть – метал.
____________________
Деякі
метали не тверді.
ІV. М – Р. Ця фігура
застосовується рідко, оскільки хід мислення у ній
S – М. дивний та незвичайний.
Наприклад:
S – Р.
Усі метали – матеріальні речі
Усі матеріальні речі мають
вагу.
_____________________________
Модуси
категоричного силогізму
У кожній фігурі можна виділити також модуси,
тобто комбінації з 4-х видів суджень А, Е, І, О. Наведемо ще раз відомий вам
силогізм про залізо:
А Усі
метали проводять електрику.
А Залізо – метал.
_____________________________
А Залізо
проводить електрику.
Більший засновок тут загальноствердне
судження А, менший засновок – теж загальноствердне судження А і висновок – теж
А. Модус цього силогізму записується ААА. Отже,
модусами фігур
категоричного силогізму називаються різновиди силогізму, які відрізняються
один від одного якісною характеристикою засновків та висновку, що входять до
них.
Якщо комбінувати з чотирьох різновидів
суджень (А, Е, І, О) по три, то виходить 64 можливих варіанти для кожної
фігури, а з урахуванням того, що фігур – 4, то 256. Але більшість таких
сполучень суперечать як загальним правилам, так і правилам окремих фігур
силогізму. Мають сенс лише 11 комбінацій, а оскільки деякі з них повторюються у
різних фігурах, то правильними є 19 модусів:
І фігура: ААА, ЕАЕ, АІІ, ЕІО.
ІІ
фігура: АЕЕ, АОО, ЕАЕ, ЕІО.
ІІІ фігура: ААІ, ЕАО,
ІАІ, ОАО, АІІ, ЕІО.
ІV фігура: ААІ, АЕЕ, ІАІ, ЕАО, ЕІО.
Кожен із цих модусів має свою
мнемонічну назву (тобто призначену для запам’ятовування). Голосні букви у цих назвах послідовно виражають символи
суджень, що складають засновки і висновок силогізму. Ці назви такі:
І.Barbara, Celarent, Darii, Ferio.
II. Cesare, Camestres, Festino, Baroco.
III. Darapti, Disamis, Datisi, Felapton, Bocardo.
IV. Bramantip, Camenes, Dimares, Fesapo, Fresison.
Наведемо
приклади кожного модусу І фігури як найбільш застосовуваної.
Barbara
А Усі
метали проводять електрику.
А Залізо – метал.
_____________________________
А Залізо
проводить електрику.
Celarent
Е Жодна
комаха не має більше 3-х пар ніжок.
А Бджола – комаха.
_______________________________________
Е Бджоли
не мають більше 3-х пар ніжок.
Darii
А Усі
хижаки їдять м’ясо.
І Деякі домашні тварини – хижаки.
____________________________________
І Деякі
домашні тварини їдять м’ясо.
Ferio
Е Жоден
страус не літає.
І Деякі птахи – страуси.
____________________________________
О Деякі
птахи не літають.
Перша фігура найбільш типова для
дедуктивного умовиводу, особливо її перший модус ААА. Модуси першої фігури
дають висновки усіх чотирьох видів суджень. Особливу цінність має
загальноствердний висновок, якого не може дати ніяка інша фігура силогізму. В
умовиводах за цією фігурою найбільш яскраво розкривається аксіома силогізму,
правильність висновку тут легко перевірити. Тому висновки за іншими фігурами
стараються зазвичай звести до модусів першої фігури силогізму.
Умовні силогізми
Умовним силогізмом називається такий силогізм, де більший засновок представлений умовним
судженням. Виділяються два види умовних силогізмів – конструктивний та
деструктивний.
1. Конструктивний силогізм:
Якщо А є В, то С є D
А є В
_______________________
С є D
2. Деструктивний силогізм:
Якщо А є В, то С є D
С є не є D
_______________________
А не є В
Правило:
в умовних силогізмах можна робити висновки лише від ствердження основи до
ствердження наслідку та від заперечення наслідку до заперечення основи.
Робити висновки від заперечення
основи до заперечення наслідку та від ствердження наслідку до ствердження
основи не можна, оскільки наслідки можуть бути викликані й іншими причинами.
Незнання цього правила часто веде до неприємних наслідків.
Наприклад, мати, що чекає сина, який затримався на вечірці, може мислити з
логічною помилкою:
Якщо син попав під машину,
то він не прийде вчасно додому.
Син не прийшов вчасно додому.
_____________________________
Скорочений силогізм (ентимема)
У повсякденній мові силогізм частіше за все
висловлюють не у розгорнутому вигляді, а скорочено, випускаючи один із
засновків або висновок.
Силогізм
із пропущеним засновком або висновком називають скороченим силогізмомабо ентимемою (що у перекладі з грецької буквально означає «у розумі»).
Частіше
за все випускається більший засновок, як такий, що найлегше дорозумлюється, і
висловлюються лише менший засновок і висновок. Візьмемо для прикладу вже добре
відомий нам силогізм про залізо: «Залізо – метал. Отже воно проводить
електрику». Тут дорозумлюється більший засновок: «Усі метали проводять
електрику».
Але
може випускатися й менший засновок («Усі метали проводять електрику, отже,
залізо – також») і навіть висновок («Усі метали проводять електрику, а залізо –
метал»). Для перевірки правильності ентимем їх треба розгортати у повні
силогізми.
3. Індуктивні умовиводи
Індукція – це
умовивід, у якому на основі знання частини предметів класу робиться висновок
про всі предмети класу, про клас у цілому.
Приклад
індукції:
У першому філіалі банківського об’єднання порушень
фінансової дисципліни не виявлено.
У
другому філіалі банківського об’єднання порушень фінансової дисципліни не виявлено.
У
третьому філіалі банківського об’єднання порушень фінансової дисципліни не виявлено.
До складу банківського об’єднання входять лише три філіали.
______________________________________________________
У
всьому банківському об’єднанні порушень фінансової дисципліни не виявлено.
Індукція
буває повною та неповною.
Повна індукція – це умовивід, у якому на основі
належності до кожного елемента або кожної частини класу певної ознаки робиться
висновок про його належність до класу в цілому.
Повна
індукція можлива лише тоді, коли ми маємо справу із закритими класами,
кількість елементів у яких кінечна та може бути легко оглянута. Повною
індукцією є наведений вище приклад, де членів класу взагалі «один, другий і
кінець».
В
інших випадках індукція неповна.
Неповна індукція поділяється на популярну та наукову.
Популярна індукція найбільш недостовірна; висновки, що за її допомогою
отримуються, можна назвати проблематичними, або вірогідними. Приклад популярної
індукції: «Існують лише білі лебеді, тому що чорних ми ніколи не бачили». Але
після відкриття Австралії виявилося, що існують і чорні лебеді.
Для
підвищення достовірності знань, отриманих за допомогою індукції, розроблені
методи наукової індукції.
Науковою
індукцією називають умовивід, у якому узагальнення будується
шляхом відбору необхідних та виключення випадкових обставин.
Індуктивні
умовиводи досліджують причину явищ. Існують 5 методів вивчення причини явищ.
1. Метод
схожості, або згоди. Полягає він у такому:
Якщо
для двох або більше предметів є загальною лише одна обставина, то вона й є
причиною даного явища.
Наприклад,
три людини заразилися дизентерією. При з’ясуванні
джерела захворювання головна увага зверталася на вживання тієї води та
продуктів, від яких улітку можна найчастіше заразитися дизентерією: питна вода
з колодязів, вода з річки, молоко, овочі, фрукти. Спільним для усіх трьох
виявилося лише вживання молока, а значить, найбільша вірогідність заразитися
була від молока. І точно, коли перевірили продавщицю цього молока, то вона
виявилася бацилоносієм дизентерії. Тобто, у даному випадку індукція привела до
вірного висновку.
2. Метод різниці.
За методом різниціпорівнюють два випадки, в одному з яких досліджуване явище настає, а у другому
не настає, при цьому другий випадок відрізняється від першого лише однією
обставиною, а усі інші є схожими.
Цим методом була встановлена причина
різної швидкості падіння тіл – наявність атмосфери. Коли з циліндра, у якому
містилися різні тіла, було відкачане повітря, то виявилося, що й вата, і
свинець падають з однаковою швидкістю.
3. Іноді застосовують з’єднаний
метод схожості та різниці, який являє собою комбінацію перших двох
методів, коли шляхом аналізу багатьох випадків виявляють як схоже у різному,
так і різне у схожому.
Приклад: якби ми досліджували не
лише тих, хто заразився дизентерією, але й тих, хто не заразився, то побачили
б, що усі вони не вживали молока. Це й було б застосування з’єднаного метода.
4. Метод супровідних
змін.
Якщо зміна однієї
обставини завжди викликає зміни іншої обставини, то перша обставина й є
причиною досліджуваного явища.
Не завжди, правда, можна
усунути якусь обставину. Дію Місяця на Землю не припиниш. Але можна помітити,
які явища спостерігаються, коли Місяць змінює своє місцезнаходження. Так було
встановлено, що вплив Місяця є причиною припливів та відпливів.
5. Метод залишків.
Якщо відняти від даного
явища ту частину, що відома як дія певних обставин, можна встановити причину
частини, що лишилася.
Так була відкрита планета
Нептун. Відняли вплив на орбіту Урана відомих планет, але лишилася ще одна
невідома величина. Було висловлене припущення, що ця величина пов’язана з
наявністю ще однієї невідомої планети. Лавер’є розрахував, де вона знаходиться,
а астроном Галлє знайшов її у цьому місці, побудувавши більш потужний телескоп.
4. Умовиводи за аналогією
Аналогія – умовивід про
належність до предмета певної ознаки на основі схожості в ознаках з іншим
предметом.
Умовиводами за аналогією
часто користуються геологи. Схожість ландшафту місцевості, де була знайдена
нафта, з ландшафтом місцевості, де йде геологорозвідка, дозволяє висловити
припущення, що і в другому випадку у надрах землі є нафта. Але висновки за аналогією
завжди вірогідні. Застосування аналогії часто призводить до помилкових
висновків, що навіть породило афоризм: «Принцип аналогії – це такий прийом
пізнання, що кульгає на обидві ноги». Так, відомий філософ І. Кант, порівнюючи
Землю та Місяць, убачив ряд спільних для цих небесних тіл ознак і на цій основі
зробив припущення, що Місяць заселений. Та нині ми знаємо, що він помилився.
Виключення складає лише так
звана строга аналогія. Відмітна її особливість – необхідний зв’язок
ознаки, що переноситься, з ознаками схожості. Але строга аналогія являє
собою сполучення аналогії з дедукцією. Припустимо, один предмет має ознаки а, b, c, d, е, другий предмет – ознаки а, b, c, d. Для того, щоб ознаку е перенести на
другий предмет, треба, щоб наявність ознаки е з необхідністю логічно випливала
з однієї з ознак а, b, c, d або з кількох одразу.
У
всіх інших випадках аналогія буде нестрогою. Умовами, що підвищують ступінь
вірогідності висновків у нестрогій аналогії, виступають:
1)
схожість уподібнюваних предметів у значній кількості істотних ознак (чим
більше, тим краще);
2)
відсутність істотних відмінностей між уподібнюваними предметами;
3)
великий ступінь вірогідності знання про залежність між схожими ознаками та
ознакою, що переноситься.
Рекомендована література
1. Бочаров
В.А Аристотель и традиционная логика. – М., 1984.
2. Бочаров
В.А., Маркин В.И. Основы логики. – М.:
Изд-во, “Инфра-М”, 1997.
3. Гетманова
А.Д. Учебник по логике. – М., 2002.
4. Горский
Д.П., Ивин А.А., Никифоров А. А. Краткий
словарь по логике. – М., 1991.
5. Ерышев
А.А., Лукашевич Н.П., Сластенко Е.Ф. Логика. – К.: МАУП, 2000.
6.Иванов Е.А. Логика. – М., 2001.
7. Ковальски
Р. Логика в решении проблем. – М.: “Наука”, 1990.
8.Кириллов В.И., Старченко А.А. Логика. – М.,
1995.
9. Литвак М.Е. Как узнать и изменить свою судьбу. – Ростов-на-Дону: Феникс,
2002.
10. Светлов В.А. Практическая логика. – М., 1997.