ТЕМА 8. Логічні основи теорії доведення
Зміст сторінки:
ТЕМА 8. Логічні основи теорії доведення
5. Основні помилки в доведенні
Сутність доведення
Як уже говорилося вище, усі явища і предмети дійсності
взаємозумовлені, ніщо не виникає з нічого, усе змінюється та розвивається на
основі чогось. Це дозволяє й мисленню, оскільки воно відображує дійсність, одні
думки обгрунтовувати на других, зумовлювати другими, доводити їх.
Відкриваючи істину, людина прагне передати її іншим
людям. А для цього вона повинна сама переконатися в її істинності та переконати
у ній інших, оскільки більшість істин не носять очевидний характер. Очевидні
лише істини факту, які ми отримуємо за допомогою наших органів почуттів, наприклад «трава зелена» або «у цій аудиторії
тепло». Величезна ж більшість істин не настільки очевидна
і, отже, передбачає доведення. Інакше не було б необхідності у науці, бо наука
без доведення не існує.
Що ж таке доведення
Під доведенням розуміється форма мислення, в якій на
основі істинності одних знань розкривається істинність або хибність інших.
У мові доведенню відповідає сукупність речень, певним
чином пов’язаних між собою, які
виражають ланцюг умовиводів.
У чому схожість та різниця між умовиводом та доведенням
Також, як і умовивід, доведення спрямоване на отримання опосередкованого,
вивідного знання. Але якщо умовивід спрямований на те, щоб вивести нове знання,
то доведення – на те, щоб установити істинність або хибність того чи іншого
знання. Ось чому вважається, що доведення служать важливим засобом формування
наших переконань – тобто впевненості у правоті тих чи інших знань.
Структура доведення
Будь-яке доведення, незалежно від
його конкретного змісту, має однакову структуру. Завжди є перше – те, що
доводиться, друге – чим доводиться і третє – як, яким чином доводиться.
1. Теза доведення. Це положення, істинність або
хибність якого обгрунтовується за допомогою даного доведення.
В якості тез можуть
виступати найрізноманітніші судження, якщо вони не очевидні й потребують
доведення. У науці – це різні наукові положення, що мають те чи інше теоретичне або практичне значення.
Різновидом тези
виступає гіпотеза (від грецьк. hypothesis – основа, припущення, догадка). Це й не
істинне й не хибне судження, а більш-менш правдоподібне припущення, яке з часом
може стати предметом доведення, а з часом набути статусу наукового положення
або теорії.
2. Основи доведення
(або аргументи, докази). Це положення, з яких виводиться істинність або
хибність тези.
Відрізняють різні види основ.
2.1. Факти. І. Павлов називав їх повітрям ученого.
2.2. Визначення. Наприклад, у геометрії визначення
вихідних понять – точки, лінії, площини – має фундаментальне значення для
наступного доведення теорем. Визначення здатні служити основою доведення тому,
що розкривають як загальні (родові), так і відмітні (видові) істотні ознаки
предмета, якими можуть викликатися інші властивості або ознаки. Особливо велике
значення мають визначення найбільш загальних понять.
2.3. Аксіоми та постулати. Вимоги до аксіом:
а) їх несуперечність одна одній;
б) їх незалежність одна від одної;
в) повнота їх системи, тобто самодостатність.
2.4. Раніше доведені положення.
Звичайно усі ці види основ застосовуються у різних
сполученнях.
3. Демонстрація – це виведення тези з аргументів.
Щоб доведення відбулося, необхідний послідовний логічний
зв’язок основ та висновків із цих основ, у результаті чого з необхідністю
визнається істинність або хибність тези. А раз “із необхідністю”, то це
означає, що основою всякого доведення є дедукція. Часто доведення – це форма,
зворотня силогізму. Якщо побудувати доведення у вигляді класичного ланцюжку
умовиводів – спочатку наводяться всі засновки, всі проміжні висновки і лише
наприкінці – теза, яка обгрунтовувалася, то слухати таку промову зазвичай нуднувато.
Якщо одразу не зрозумів, до чого хилить оратор, важко слухати уважно, а коли
зрозумів – стає нецікаво. Тому спочатку краще сформулювати тезу, і тільки потім
приступати до її доведення. Якщо я згодний з оратором, то одразу переймуся до
нього повагою (якщо він думає, як я, значить, розумний) і прислухаюся до його
аргументів. Вони можуть і відрізнятися від моїх. Якщо ж не згодний, то буду
уважно слухати, щоб знайти спростування. А може, він мене й переконає.
Таким чином, у доведенні за відомим висновком – тезою
відновлюються засновки виведення – аргументи.
Яким би великим не було значення дедукції у доведеннях,
вони не можуть обійтися й без індукції, оскільки у процесі доведення ми
звертаємося до фактів, отриманих
досвідним шляхом. У комплексі з іншими способами доведення може
застосовуватися й аналогія.
Такі основні компоненти доведення.
Якщо тепер позначити літерою Т тезу, літерою А –
аргументи, а відношення між ними – знаком імплікації, то загальна формула
доведення буде виглядати так:
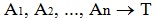
Види доведень
Основи, за якими доведення подляються
на види, це мета доведення і спосіб доведення.
За метою доведення поділяються на доведення у власному
значенні слова та спростування.
Доведення у
власному значенні слова (або підтвердження) – обгрунтування істинності тези.
Величезна більшість доведень у науках має саме такий характер.
Спростування – це обгрунтування хибності
тези, яке досягається за допомогою тих же істинних доказів.
Спростування може
приймати різні форми. Це може бути:
1. Спростування
тези.
2. Критика основ
(аргументів).
3. Обгрунтування
відсутності зв’язку між аргументами та тезою.
Досить часто
спростування має всебічний характер, воно торкається одразу всіх компонентів
доведення.
За способом
доведення відрізняють два види доведень: прямі та непрямі.
Прямим називають доведення тези без
звернення до конкуруючих із цією тезою припущень. У ньому докази безпосередньо
обгрунтовують істинність або хибність тези. Тут усе зрозуміло.
Непрямим називають доведення тези шляхом
установлення хибності антитези або інших конкуруючих із тезою припущень.
Існують два види непрямого доведення:
апагогічне та розділове.
Апагогічним (від грецьк. “той, що відводить, уводить”)
називають обгрунтування тези шляхом установлення хибності допущення, що
суперечить їй – антитези.
При наявності тези Т висувають суперечну їй – 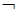 Т і припускають, що вона істинна (говорять: припустимо, істинним є
Т і припускають, що вона істинна (говорять: припустимо, істинним є
не-Т). Далі виводять наслідки, що випливають із неї та перевіряють їх. Якщо
буде встановлено, що виведені з антитези наслідки у дійсності не існують і їх
існування взагалі немислиме (абсурдне)
або вони суперечать раніше доведеним положенням, то тим самим буде доведена
хибність антитези 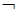 Т.
Т.
Висновок про хибність антитези робиться на основі
правила умовного силогізму: з хибності наслідку з необхідністю випливає
хибність основи. Довівши хибність 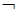 Т за законом
Т за законом
виключеного третього переходять до істинності тези Т.
Апагогічне непряме доведення називають іще зведенням до
абсурду. У математиці та деяких інших науках воно отримало назву доведення від
супротивного.
Розділовим називають непряме
доведення тези, при якому з кількох можливих тез методом виключення доводиться
одна.
На відміну від апагогічного, у розділовому доведенні
фігурують не два (Т і 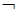 Т), а кілька
Т), а кілька
положень, наприклад, Т, В, С, кожне з яких є членом закритої диз’юнкції.
Наприклад, злочин могли скоїти лише три людини і ніхто
інший. Обгунтування тези будується у цьому випадку методом виключення. У
процесі доведення показують неспроможність усіх членів диз’юнкції, крім одного
(Т). Тим самим опосередковано доводять істинність тези, що лишається.
Розділове доведення спроможне лише у тому випадку, якщо
диз’юнкція закрита. Якщо ж розглядаються не всі варіанти розв’язання, то метод
виключення дає лише проблематичний висновок.
Правила
доведення
1. Правила по відношенню до тези.
1.1. Визначеність тези. Теза повинна бути
сформульована ясно й чітко.
1.2. Теза повинна лишатися тотожною, тобто
однією й тією ж протягом усього доведенняє
1.3. Теза не повинна містити логічної
суперечності.
1.4. Теза не повинна перебувати у логічній
сцперечності з висловленними раніше судженнями з даного питання.
1.5. Теза повинна бути
обгрунтована фактами.
1.6. Тезою не повинне бути судження очевидне,
оскільки те, що достовірне саме по собі, не потребує доведень.
1.7. Теза повинна визначити
весь хід доведення так, щоб те, що доведено, було саме тим, що потрібно було
довести.
2.
Правила відносно аргументів.
2.1. Аргумент повинен
бути судженням істинним.
2.2. Аргумент
повинен бути достатньою основою для
положення, що доводиться.
2.3. Істинність аргумента повинна бути
доведена самостійно, незалежно від положення, що доводиться.
3.
Правило відносно демонстрації.
Оскільки
демонстрація завжди здійснюється у формі того чи іншого умовиводу, вона повинна
відповідати правилам умовиводів.
Якщо доведення відповідає усім правилам логіки, воно називається
доведенням до істини.
Основні помилки у
доведенні
1.
Помилки відносно тези.
1.1.
Підміна тези. Буває повна, коли у кінцевому підсумку пропонент обгрунтовує щось
інше, ніж висунув спочатку, або неповна, коли він звужує або пом’якшує своє
первісне надто загальне твердження.
1.2. Доведення до людини. Теза підміняється міркуваннями про
компетентність або некомпетентність експертів.
1.3.
Доведення до натовпу – спроба викликати у людей певні почуття та емоції по відношенню
до тези або до антитези і цим переконати.
2.
Помилки відносно аргументів.
2.1.
Хибний аргумент.
2.2. Випередження основи –
аргумент не є явно хибним, але не доведений.
2.3.
Хто багато доводить, той нічого не доводить. По відношенню до аргументів «краще
менше, та краще».
3.
Помилки, пов’язані з демонстрацією.
У
першу чергу – це помилки в умовиводах.
3.1. Теза не випливає з аргументів.
3.2.
Від сказаного відносно до сказаного абсолютно. Наприклад, судження «Бухгалтери
знають правила бухгалтерського обліку» істинне у принципі, але не для кожного
конкретного випадку
3.3. Доведення не повинне робити коло.
Сюди
ж відносяться аргументи до сили, до невігластва (використання необізнаності
опонента), до вигоди, до здорового глузду (а фактично, до буденної свідомості).
Говорячи
про логічні помилки, звичайно мають на увазі ненавмисні порушення правил логіки
у процесі міркування з причини логічної неуважності або необізнаності. Такі
помилки називають паралогізмами. Навмисні порушення логічних правил з метою
ввести в оману опонента та слухачів, щоб створити видимість перемоги у
дискусії, називають логічними хитрощами або софізмами.
З
давніх часів до нас дійшли софізми, які застосовувалися для обгрунтування
очевидних дуростей. Наприклад: «Чого ти не загубив, те маєш. Роги ти не
загубив. Значить, роги в тебе є». «Той, хто сидів, устав; хто встав, той
стоїть; тому той, хто сидить, стоїть». «Цей пес – твій; він – батько; значить,
він – твій батько». Софізми використовують багатозначність слів, підміну понять
та інші логічні помилки. Давньоримський філософ порівнював софістів з
фокусниками: ми розуміємо, що нас дурять, але як – не розуміємо. Хоча,
звичайно, зрозуміти можна. Наприклад, у софізмі про роги обігрується
двозначність поняття «не загубив», яке може означати «мав і не загубив» і «не
мав і не загубив».
Крім
паралогізмів та софізмів існують також парадокси.
Парадокс – це
міркування, яке одночасно доводить істинність прямо протилежних суджень.
Парадокси пов’язані не
з усвідомленими помилками, а з особливостями самого мислення. Найзнаменитіший
(з давнини) парадокс – «Я брешу». Якщо я визнаю, що я брешу – то це вже не
брехня. Але якщо це правда, то виходить, що я все-таки брешу, і так за колом до
безкінечності.
Рекомендована
література
1. Асмус В.Ф. Учение логики о
доказательстве и опровержении. – М., 1954.
2.
Горский Д.П., Ивин А.А., Никифоров А. А.
Краткий словарь по логике. – М., 1991.
3.
Ерышев А.А., Лукашевич Н.П., Сластенко Е.Ф. Логика. – К.: МАУП, 2000.
4.
Иванов Е.А. Логика. – М., 2001.
5.
Івін О.А. Логіка. – К.,1996.
6.
Кириллов В.И., Старченко А.А. Логика. – М., 1995.
7. Литвак М.Е. Как узнать и изменить свою судьбу. – Ростов-на Дону:
Феникс, 2002.
8. Рузавин Н.В. Логика и аргументация. – М., 1997.
9. Эйсман А.А. Логика доказывания. – М., 1997.