ТЕМА 5. Складні судження
Зміст сторінки:
ТЕМА 5. Складні судження
1. Класифікація складних суджень
2. Умови істинності або хибності складних суджень
Класифікація складних суджень
У попередній лекції уже
згадувалося, що крім простих суджень існують також складні. Розрізняють такі
види складних суджень: з’єднувальні, розділові, умовні й еквівалентні.
1. З’єднувальним
(кон’юнктивним) судженням називають судження, що складається з кількох простих, пов’язаних логічним сполучником «і».
Наприклад, судження
«Яблука і груші належать до фруктів», є з’єднувальним судженням, що складається
з двох простих: «Яблука належать до фруктів» і «Груші належать до фруктів».
У природній мові
кон’юнктивний сполучник може бути представлений і такими висловлюваннями, як
«та», «а», «але», «а також», «як і», «хоча», «однак», «незважаючи на»,
«одночасно» та іншими. Нарешті, він може взагалі матися на увазі, наприклад:
«Краса проходить, таланти довго не в’януть».
З точки зору мови логіки
предикатів, з’єднувальне судження може бути виражене в одному з чотирьох видів.
1) S1 і S2 є Р. Тут підходить приклад із яблуками та грушами.
2) S є Р1 і Р2. Наприклад: «На вулиці холодно і йде дощ».
3) S1 і S2 є Р1 і Р2. Наприклад: «З поліцмейстером і прокурором Ноздрьов теж був на «ти» і
поводився по-дружньому» (Гоголь).
4) S1 є Р1 і S2 є Р2. Наприклад:
«Хто хоче що-небудь зробити – знаходить засоби, хто не хоче нічого робити –
знаходить виправдовування».
У алфавіті мови логіки
предикатів кон’юнкцію позначають так: р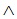 q, де р і q – члени кон’юнкції,
q, де р і q – члени кон’юнкції, 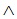 – знак кон’юнкції.
– знак кон’юнкції.
2. Розділовим, або диз’юнктивним, називають судження, що складається з кількох простих,
пов’язаних
логічним сполучником «або». Наприклад: «Або запросимо аудитора, який виправить
наші помилки, або прийде податківець і оштрафує».
У мові логіки предикатів
розділове судження може бути виражене в одному з чотирьох видів.
1) S1 або S2 є Р. Наприклад: «Іванов або Петров здає екзамен».
2) S є Р1 або Р2. Наприклад: «Іванов здає
екзамен або залік».
3) S1 або S2 є Р1 або Р2. Це буде виглядати, наприклад, так: «Іванов або Петров здає екзамен або залік».
4) S1 є Р1 або S2 є Р2. Тут
цілком підходить наш «аудиторський» приклад.
Позначається диз’юнкція:
р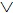 q
q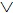 …
…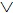 n.
n.
Диз’юнкція буває строгою і нестрогою. Це пов’язане з тим, що у нашій мові сполучник «або» може
бути застосований у двох значеннях: невиключному і виключному. Невиключне
значення передбачає, що слово «або» означає «або одне, або друге, або обидва
одразу». Наприклад, висловлювання «У цьому сезоні я хочу піти на «Пікову даму»
або на «Аїду» припускає можливість два рази відвідати оперу. А ось у висловлюванні
«Він вчиться у Московському або Петербургському університеті на денному
відділенні» мається на увазі, шо дана людина вчиться у якомусь одному з цих
університетів. Для посилення у строгій диз’юнкції сполучники використовуються
два рази: або – або, чи – чи. Наприклад: «Людина до 40 років або сама собі
лікар, або вона дурна».
Строга диз’юнкція
позначається р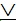 q.
q.
Серед диз’юнктивних суджень виділяють також повну и неповну диз’юнкцію.
Повним, або закритим називають диз’юнктивне судження, у якому перелічені усі ознаки або усі види певного роду. Наприклад: «Ліса бувають листвяні, хвойні або змішані». І все, обсяг даного класу вичерпаний. Символічно закриту диз’юнкцію можна записати так: р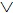 q
q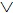 r
r
Неповним або відкритим називають диз’юнктивне судження, у якому перелічені не усі види певного роду, що виражається трьома крапками: р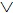 q
q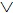 r
r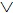 … Наприклад, якщо б ми стали перераховувати не
… Наприклад, якщо б ми стали перераховувати не
види лісів, а види дерев, то швидко б утомилися, не перелічивши усі, і
поставили б три крапки. Це й була б неповная диз’юнкція. У природній мові
неповна диз’юнкція виражається словами: і т. д., і т. ін., та ін. та іншими.
3. Умовним, або імплікативним,
називають судження, що складається з двох простих, пов’язаних логічним сполучником
«якщо…, то…» Наприклад: «Якщо запобіжник плавиться, то телевізор гасне». Перше
судження «Запобіжник плавиться» називають антецендентом (попереднім), а друге
«Телевізор гасне» – консеквентом (наступним).
У природній мові для
вираження умовних суджень застосовується не лише сполучник «якщо…, то…», але й
інші сполучники: «там…, де…», «тоді…, коли…», «остільки…, оскільки…» і т. ін.
У мові логіки предикатів
імплікація виражається так: р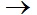 q.
q.
4. Еквівалентнимсудженням (або подвійною імплікацією) називають судження, що складається
з двох простих, пов’язаних подвійною (прямою та зворотньою) умовною залежністю,
яка виражається логічним сполучником «якщо і тільки якщо…, то…» Наприклад:
«Якщо і тільки якщо людина нагороджена орденами та медалями, то вона має право
на носіння відповідних орденських планок».
У природній мові для
вираження еквівалентних суджень застосовуються й інші сполучники: «лише при
умові, що…, то…», «у тому, і тільки у тому випадку, коли…, тоді…», «тільки
тоді, коли…, то…» та інші. У мові логіки предикатів еквіваленція позначається:
р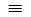 q або р
q або р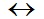 q.
q.
Умови істинності або хибності складних суджень
Досі ми розглядали
судження (та й інші логічні категорії) лише з точки зору формальної логіки
предикатів. Подивимося тепер на складні судження з погляду логіки висловлювань,
у якій розглядається істинність та хибність суджень.
Почнемо зі з’єднувальних
(кон’юнктивних) суджень. З’єднувальне судження істинне при істинності усіх
складаючих його кон’юнктів і хибне при хибности хоча б одного з них. Умови
істинності суджень можна представляти у вигляді так званих таблиць істинності.
Для з’єднувального судження таблиця істинності буде мати такий вигляд:
|
р |
q |
р |
|
і |
і |
і |
|
і |
х |
х |
|
х |
і |
х |
|
х |
х |
х |
(Замість «і» та «х»
іноді пишуть «1» та «0»).
Саме така умова
істинності кон’юнкцій витікає з того, що «р і q» можна замінити, наприклад, на
«як р, так і q», тому для того, щоб усе судження було істинним, обидві його
частини повинні бути істинним.
Для розуміння логіки
висловлювань треба запам’ятати таке правило: усі висловлювання у ній або
істинні, або хибні, третього не дано.
Наприклад, візьмемо таке
висловлювання: «Через 5 років тут буде дощ з громом». Воно здається нам
невизначеним з точки зору істинності, але у логіці висловлювань невизначеності
не буває.
Така ж сама справа й зі складними висловлювання. У звичайній мові ми пов’язуємо сполучником «і» два висловлювання, котрі, як нам здається, пов’язані якимось значенням. Але значення – поняття суб’єктивне, для когось воно є, а для когось – ні. Тому логіка висловлювань таке поняття, як «змістовні зв’язки», відкидає. Наприклад, висловлювання «Він ішов у пальті, і я йшов до університету» нам здається безглуздим, тому воно не може бути істинним або хибним. Але з точки зору логіки висловлювань, якщо обидві його частини істинні, то воно істинне. Так же само істинне й складне судження «2 – просте число й Москва – велике місто». Але якщо ми скажемо «2 – непарне число й Москва – велике місто», то усе судження перетворюється на хибне.
Перейдемо тепер до умов
істинності розділових (диз’юнктивних) суджень. Вони будуть різними для
нестрогої та строгої диз’юнкції.
Нестрога диз’юнкція
істинна, коли істинний хоча б один член диз’юнкції, і хибна при хибности обох
її членів.
|
р |
q |
р |
|
і |
і |
і |
|
і |
х |
і |
|
х |
і |
і |
|
х |
х |
х |
Для строгої диз’юнкції
умови істинності будуть іншими. Істинною строга диз’юнкція буде лише при
істинності одного та хибности іншого члена. Як уже говорилося вище, у звичайній
мові, щоб підкреслити, що диз’юнкція строга, застосовують сполучник «або» 2
рази: «або р, або q». Тоді зрозуміло, що коли істинні і р, і q, або якщо обидва
хибні, то хибна й уся строга диз’юнкція. У вигляді таблиці істинності це
зображується так:
|
р |
q |
р |
|
і |
і |
х |
|
і |
х |
і |
|
х |
і |
і |
|
х |
х |
х |
Умовні (імплікативні)
судження істинні в усіх випадках, окрім одного: при істинності антецендента та
хибности консеквента (2-й рядок):
|
р |
q |
р |
|
і |
і |
і |
|
і |
х |
х |
|
х |
і |
і |
|
х |
х |
і |
Наприклад: «Якщо
запобіжник плавиться, то телевізор не гасне». Антецендент істинний, але
висновок з нього робиться хибний, тому вся імплікація хибна.
У решті ж випадків
імплікація буде істинною. У першому випадку це найбільш очевидне. З істинного
антецендента («Запобіжник плавиться») робиться істинний же висновок («Телевізор
гасне»).
Але імпликація істинна і
ще у двох випадках, хоча, на перший погляд, це може здатися дивним. Візьмемо
перший випадок: антецендент хибний, консеквент істинний. У цьому випадку
імплікація буде істинною, навіть якщо ми візьмемо такий приклад: «Якщо 2х2=5,
то деякі слони живуть в Африці». Ця імплікація є істинною тому, що деякі слони
дійсно живуть в Африці, поза залежністю від будь-яких умов, істинних або
хибних. Але якщо ми поміняємо антецендент і консеквент місцями: «Якщо деякі
слони живуть в Африці, то 2х2=5», ми отримуємо 2-й рядок таблиці істинності:
імплікація хибна, тому що 2х2 ніколи не буде 5, поза залежністю від будь-яких
умов, навіть істинних.
І, нарешті, останній
рядок. Якщо і р, і q хибні, то імплікація буде істинною навіть у такому
випадку: «Якщо 2х2=5, то я – папа римський», оскільки істинність імплікації
залежить не від змісту висловлювань, які входять до неї, а лише від їх
взаємовідношень між собою. Тут імплікація буде істинною, оскільки хибність
одного не ставить під сумнів хибність іншого.
Еквівалентні судження
(подвійна імплікація) істинні у тих випадках, коли обидва судження приймають
однакові значення, будучи одночасно або істинними, або хибними (1-й та 4-й
рядки).
|
р |
q |
р |
|
і |
і |
і |
|
і |
х |
х |
|
х |
і |
х |
|
х |
х |
і |
Це значить, що
істинність р достатня для визнання істинним q, а істинність q достатня для
визнания істинності р. Те ж саме буде й при їх хибності. Тому приклад з 2х2=5 і
папою римським буде істинним висловлюванням і для подвійної імплікації. А ось у
решті випадків подвійна імплікація буде хибною. Чому – я думаю, розберетеся самі.
Окрім відношень кон’юнкції, диз’юнкції, імплікації та еквіваленції у логіці висловлювань застосовується також відношення заперечення. Повний зміст відношення заперечення задається умовою: якщо висловлювання р істинне, то його заперечення (не-р) хибне, і якщо р – хибне, то не-р – істинне. Відношення заперечення позначається  р. Для заперечення
р. Для заперечення
теж можна побудувати таблицю істинності:
|
р |
|
|
і |
х |
|
х |
і |
Знаючи (і розуміючи)
таблиці істинності для елементарних складних висловлювань, можна будувати їх і
для більш складних, що складаються з них, і таким чином, визначати умови
істинності для будь-якого виразу. Наприклад, треба побудувати таблицю
істинності для такого виразу: ( А
А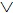 В)
В)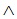 (В
(В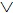 С). Будувати ми її будемо у такому порядку: спочатку задамо усі можливі
С). Будувати ми її будемо у такому порядку: спочатку задамо усі можливі
комбінації істинності й хибності А, В і С. Потім розберемо, як розв’язується
таблиця істинності на прикладі першого рядка.
Спершу починаємо з чого
З не-А. Якщо А істинне, то не-А – хибне. Далі переходимо до диз’юнкції у перших
дужках, «не-А або В». Якщо хоча б одне з них істинне, то весь вираз істинний. У
нашому першому рядку істинні обидва. Пишемо «1». Аналогічно «В або С», теж
нестрога диз’юнкція й обидва істинні, значить, і вона істинна теж. І, нарешті,
весь вираз, кон’юнкція. Ліва частина істинна, права частина істинна, значить,
уся кон’юнкція істинна. Користуючись цим прикладом, зробите ті таблиці
істинності, які дані вам у «Практичних завданнях».
Якщо при будь-яких
варіантах істинності та хибності змінних у всіх рядках таблиці виходить «істина»,
то такий вираз називається тотожньо-істинним, якщо у всіх рядках виходить
«хиба» – тотожньо-хибним, якщо зустрічаються обидва значення – нейтральним.
Рекомендована література
1. Берков В.Ф. Логика. –
Минск, 2002.
2. Бочаров В.А. Основы
логики. – М., 1997.
3. Гетманова А.Д.
Учебник по логике. – М., 2002.
4. Горский Д.П., Ивин
А.А., Никифоров А.А. Краткий словарь по
логике. – М., 1991.
5. Івін О.А. Логіка. –
К., 1996.
6. Кириллов В.И.,
Старченко А.А. Логика. – М., 1995.
7. Конверський А.Є.
Логіка. – Київ, 2004.
8. Литвак М.Е. Как
узнать и изменить свою судьбу. – Ростов-на – Дону: Феникс. 2002.
9. Мельников В.Н.
Логические задачи. – К. – Одесса, 1989.
10. Светлов В.А.
Практичекая логика. – М., 1997.
11. Упражнения по
логике. / Под редакцией В.И. Кириллова/. – М., 1992.