ТЕМА 3. Логічні відношення та операції над поняттями

ТЕМА 3. Логічні відношення та операції над поняттями

1. Відношення між поняттями

2. Операції над поняттями

 

1. Відношення між
поняттями

Порівнюваними називають поняття, що мають
певні ознаки, які дозволяють ці поняття між собою порівнювати. Наприклад, преса
і телебачення є порівнюваними, вони
мають спільне родове поняття «засоби масової інформації».

Непорівнюваними називають поняття, що не мають спільних ознак,
тому й порівнювати їх одне з другим неможливо. Наприклад, «душа» й «трикутник»,
«злочин» і «космос», «держава» та «симфонія». Вони належать до різних, вельми далеких одна
від другої галузей, не мають спільного родового поняття, на основі якого їх можна було б співставляти
одне з другим.

У логичному відношенні можуть знаходитися лише порівнювані поняття. Правда,
ступінь порівнюваності теж може бути різним. Наприклад, що спільного між настільки, начебто,
відмінними поняттями, як «космічний корабель» і «авторучка» І ті, й другі –
витвір людського генія. Здатність знаходити спільне у зовсім, здавалося б,
неспівставлюваних поняттях – ознака геніальності і служить логічною основою
дотепності. Наприклад, у Козьми Пруткова: «Базіка схожий на маятник: і той, і
другий треба зупинити». «Спеціалист подібний до флюсу: повнота його однобічна».
Зате інколи, навпаки, начебто, близькі за змістом поняття виявляються
непорівнюваними, наприклад, «підприємство» і «адміністрація підприємства». А ми
тепер перейдемо до подальшого вивчення порівнюваних понять.

Порівнювані поняття поділяються на сумісні та
несумісні.

Поняття, обсяги яких повністю або частково
співпадають, називаються сумісними. Існують три види відношення
сумісності:

1) тотожність;

2) перетин (перехрещування);

3) підпорядкування
(субординація).

1. У відношенні тотожності знаходяться
поняття, у яких мислиться один і той же предмет. Обсяги цих понять повністью
співпадають (хоча зміст різний). У відношенні тотожності знаходяться,
наприклад, поняття Персія та Іран (Іран раніше називався Персією), Ленінград та
Санкт-Петербург, автор «Євгенія Онєгіна» і Пушкін.

Відношення між поняттями прийнято зображувати за
допомогою колових схем, які називаються колами Ейлера. Кожне коло у них означає
обсяг поняття, а кожна точка всередині цього кола – предмет, який під цей обсяг
підпадає.

Так, відношення між двома тотожними поняттями
повинне бути зображене у вигляді двох повністю співпадаючих кіл А й В:

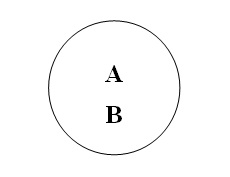
2. Відношення перетину (перехрещування).
Напевне, суть його зрозуміла вже з самої назви – їх обсяги частково
перетинаються, тобто обсяг одного частково входить до обсягу іншого і навпаки.
Зміст цих понять різний.

Наприклад, у відношенні перетину знаходяться
поняття «економіст» (А) і «викладач» (В): деякі викладачі є економістами (також
як деякі економісти – викладачами). За допомогою колових схем це відношення
зображується у вигляді двох кіл, що перетинаються:

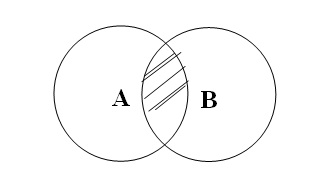
У частині кіл, що співпала (заштрихована частина
схеми) мисляться ті економісти, які є викладачами, у частині кола А, що не
співпала – економісти, що не є викладачами, у частині кола В, що не співпала –
викладачі, що не є економістами.

3. У відношенні підпорядкування (субординації) знаходяться поняття, обсяг одного з яких повністю входить до
обсягу іншого, складаючи його частину.

У такому відношенні знаходяться, наприклад,
поняття «економіст» та «бухгалтер». Обсяг одного поняття ширше обсягу другого
поняття, адже крім бухгалтерів є багато інших економістів. Понятте «бухгалтер»
повністю входить до обсягу поняття «економіст»:

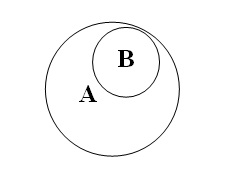
Поняття, що має більший обсяг і включає обсяг
іншого поняття, називається підпорядковуючим (А), поняття, що має менший обсяг
і складає частину обсягу іншого поняття – підпорядкованим (В).

Якщо у відношенні підпорядкування знаходяться два
загальних поняття, то підпорядковуюче поняття називається родом, підпорядковане
– видом. Так, поняття «бухгалтер» буде видом по відношенню до поняття
«економіст». Поняття може бути водночас видом (по відношенню до більш
загального поняття) і родом (по відношенню до поняття менш загального). Так,
поняття «економіст» по відношенню до поняття «професія» буде вже не родом, а
видом. Відношення між трьома підпорядкованими одне одному поняттями можна
зобразити так:

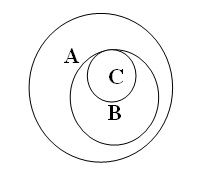
Якщо у відношенні підпорядкування знаходяться
загальне та одиничне (індивідуальне) поняття, то загальне (підпорядковуюче)
поняття є видом, а одиничне (підпорядковане) – індивідом. У такому відношенні,
наприклад, будуть знаходитися поняття «бухгалтер» і «бухгалтер Петренко».

 

Несумісні поняття

Поняття, обсяги яких не співпадають ні повністю,
ни частково, називаються неумісними. Ці поняття містять ознаки, що
виключають співпадіння їх обсягів.

Існують
три види відношень
несумісности:

1) співпідпорядкування;

2) протилежність;

3) протиріччя.

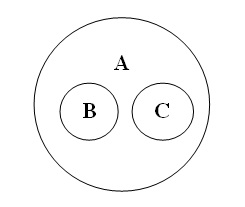
1. У відношенні співпідпорядкуваннязнаходяться два або більше понять, що не перетинаються, які підпорядковані
спільному для них поняттю. Наприклад, «ялина» (В), «береза» (С), «дерево» (А).
Поняття, що знаходяться у підпорядкуванні до спільного для них поняття,
називаються співпідпорядкованими.

У колових схемах це відношення зображується так:

2. У відношенні протилежності знаходяться
поняття, одне з яких містить певні ознаки, а друге – ознаки, несумісні з ними.
Такі поняття називаються протилежними. Обсяги двох протилежних понять складають
у сумі лише частину обсягу спільного для них родового поняття, видом якого вони
є, і якому вони співпідпорядковані. Такі, наприклад, відношения між поняттями
«чорний» і «білий», «відмінник» і «невстигаючий»:

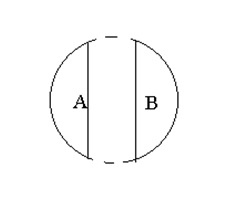
Пунктиром зображене родове поняття (скажімо,
«кольори»), оскільки воно не дане, але може бути утворене.

Поняття В містить ознаки, не сумісні з ознаками
поняття А. Обсяги цих понять не вичерпують у своїй сумі все поняття «кольори»,
тому що окрім чорного і білого існує багато інших кольорів.

3. У відношенні суперечності знаходяться
поняття, одне з яких містить певні ознаки, а друге ці ж ознаки виключає.

Обсяг двох суперечних понять складає весь обсяг
роду, видами якого вони є і якому вони співпідпорядковані.

Наприклад, якщо замість «білого» і «чорного»
візьмемо «білий» і «небілий», то відношення протилежності перетворюється на
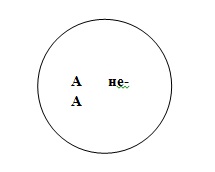
відношення суперечності. Тут уже «третього не дано»: або білий, або небілий. Графічно
це зображується так:

А не – А

У відношенні суперечності знаходиться будь-яка
пара позитивних і негативних понять: «парний» і «непарний», «дружній» і
«недружній», та деякі інші.

 

 

 

2. Операції над поняттями, їх класами

Тепер, коли ми узнали, що таке обсяг та зміст
понять, узнали їх співвідношення, ми можемо почати з ними щось робити, тобто
виконувати над ними операції. Перші дві (протилежні одна другій) – це
узагальнення та обмеження понять.

Об’єднання у більш загальні поняття називається узагальненням,
звортній процес – обмеженням:

узагальнення
———————————————————————-

ІВАНОВ – ЛЮДИНА – ПРИМАТ – ТВАРИНА – ЖИВЕ –
МАТЕРІЯ

< ———————————————————————-
обмеження

Як обмеження, так і узагальнення понять не можуть
бути безмежними. Межа узагальнення – поняття з гранично широким обсягом
(категорії). У нашому прикладі – це «матерія». Найбільш загальних категорій
усього три – річ, властивість, дія. Під одну з цих категорій підходить усе, це
межа узагальнення будь-якого поняття. Що стосується обмеження, то його межею є
одиничне поняття (у нашому прикладі – «Іванов»).

У процесі
узагальнення обсяг стає багатшим, але зміст біднішим (більш невизначеним). У
процесі обмеження – навпаки – обсяг стає біднішим, але зміст – багатшим (більш
конкретним).

Про це треба пам’ятати, коли ми хочемо донести до
когось яку-небудь думку. Чим більше ми використовуємо родових понять, тим
туманнішою виходить мова. Наприклад: «Я зайшов у помешкання, використав меблі
та посуд для того, щоб поїсти». Нічого не зрозуміло. А ось так набагато ясніше:
«Я зайшов до кафе і за стойкою бару з’їв бутерброда». У той же час зайва
детализація також може ускладнити сприйняття мови.

Обмеження та узагальнення понять не слід змішувати
з удаваним переходом від частини до цілого і виділенням частини з цілого.
Наприклад, доба поділяється на години, години на хвилини, хвилини на секунди.
Тут кожне наступне поняття не є видом попереднього, а попереднє не можна
розглядати як родове. Тому перехід від поняття «година» до поняття «доба» – не
узагальнення, а перехід від частини до цілого; перехід від поняття «година» до
поняттю «хвилина» – не обмеження, а виділення частини з цілого.

 

Визначення понять

Логічна операція, що розкриває зміст поняття,
називається визначенням.

Визначити поняття – це значить перелічити його
істотні ознаки. А оскільки істотних ознак усього дві – родова та видова, то
ясно, що визначення понять здійснюється за допомогою названня роду та видової
відмінності. «Годинник – це вимірювальний прилад, що показує час». «Шуба – це
пальто з міху».

Знання правил визначення має дуже важливе
практичне значення. Адже що найскладніше для вас, студентів Завчати напам’ять
визначення. Тепер же, розуміючи, як вони будуються, можна спробувати не зубрити
їх, а самим вникнути у суть того, як вони побудовані. І тоді, коли ви їх будете
пригадувати, вам не треба буде копатися у пам’яті, але кожного разу ви будете
ці визначення «конструювати», пригадуючи лише родові та видові ознаки поняття.

За способом виявлення змісту поняття визначення
поділяються на явні та неявні. Явні визначення утворюються за допомогою
рівності двох понять. При цьому не має значення, утворюється кожне з них одним
словом чи багатьма словами. До цього виду належали усі наведені вище приклади
визначень.

Найпоширенішим видом явних визначень є визначення
через рід та видову відмінність, про яке ми вже говорили, і його різновид –генетичне визначення. Звичайно вказувають найближчий рід, який містить
більше ознак, спільних з ознаками поняття, що визначається. Наприклад, «чек» –
це і документ, і цінний папір. Але рід «цінний папір» – ближче, а підведення
«чека» під поняття «документ» ускладнює задачу визначення. Тому таке визначення
іноді називають визначенням через найближчий рід і видову відмінність.

Генетичним (від грецького слова «генезис» –
«походження», «джерело») називається визначення, що вказує на походження
предмета, на спосіб його утворення. Наприклад: «Куля є геометричне тіло,
утворене обертанням кола навколо одного зі своїх діаметрів». Розкриваючи спосіб
утворення предмета, генетичне визначення має велике пізнавальне значення, і
тому широко використовується у науці.

Неявні визначення не мають форми прирівнювання двох понять. До них
належать: визначення через відношення до своєї протилежності, контекстуальні,
остенсивні та деякі інші.

Визначення через відношення до своєї протилежності широко використовуються при визначенні
философських категорій, тобто гранично широких понять, для яких немає
найближчого роду. Например: «Свобода є
усвідомлена необхідність». «Можливість – потенційна дійсність».

У контекстуальному визначенні зміст
розкривається у відносно самостійному уривку письмової або усної мови.
Будь-який уривок з тексту, будь-який контекст, у якому зустрічається поняття,
що цікавить нас, можна вважати неявним визначенням. Контекстуальні визначення в
основному залишаються неполними та нестійкими. Але майже усі визначення, з
якими ми стикаємося у повсякденному житті – це контекстуальні визначення.
Наприклад, почувши у розмові невідоме нам раніше слово, ми не уточнюємо його
визначення, а намагаємося самі зрозуміти його значення на основі усього
сказанного. Так само ми вчиняємо і при вивченні іноземних мов – не кидаємось
одразу ж до словника, якщо і без нього можемо зрозуміти текст у цілому і
скласти приблизне уявлення про значення незнайомих слів.

Жоден словник не здатний вичерпати усього
багатства значень окремих слів. По-справжньому будь-яке слово пізнается нами у
живій мові. Тому, якими б недосконалими не здавалися контекстуальні визначення,
лише завдяки ним ми по-справжньому володіємо мовою.

Остенсивні визначення – це визначення шляхом показу. Наприклад, до вас
звертаються з проханням пояснити, що таке зебра. Якщо вам важко це зробити, то
підводите людину до клітки з зеброю і говорите: «Це зебра». Ці визначення
нагадуют контекстуальні, але контекст тут – не шматочок тексту, а шматочок
реальності, у даному випадку – клітка з зеброю. Також, як і контекстуальні,
остенсивні визначення «грішать» незавершеністю, неостаточністю. Так, у прикладі
з зеброю ми показуємо конкретну зебру як представника усього виду зебр, не
пояснюючи, що ж саме для цього виду характерне, тобто тут одиничне злите з
загальним. Але лише остенсивні визначення пов’язують слова з речами. Без них
наша мова взагалі б не мала ніякакого сенсу, а була б пустим набором звуків.

Нарешті, у ряді випадків використовуються прийоми,
що замінюють визначення: порівняння, опис, характеристика.

Порівняння – це наочне роз’яснення предмета за допомогою порівнювання його з чимось
іншим. Той же приклад Козьми Пруткова: «Спеціалист подібний до флюсу: повнота
його однобічна». Цей прийом застосовується для образної характеристики
предмета.

Завдання опису полягає в тому, щоб найбільш
точно і повно вказати ознаки предмета (особи, події, місця, де вона відбулася).
Використовується у випадку одиничних предметів, коли неможливо вказати видову
відмінність.

Характеристика полягає у вказанні відмітних характерних (але не істотних) ознак
одиничного предмета (особи, події і т. д.) Наприклад: «Політика – це
концентроване вираження економіки». Використовується у тих же випадках, що й
опис.

Є чотири правила визначення.

1. Визначення повинне бути співмірним: обсяги
того, що визначається і того, що визначає мають бути рівними, тобто воно не
повинне бути занадто широким або занадто вузьким. Судження «Кінь – це домашня
тварина» не можна вважати визначенням, воно занадто широке. Тут не перелічені
істотні ознаки. Судження «Трикутник – це плоска фігура, яка має три рівні
сторони» також не є визначенням. Не повністю розкритий обсяг.

2. Поняття не може визначатися через саме себе.
Поняття, що визначається, не повинне повторюватися в частині, що визначає, ні
прямо, ні опосередковано.

Частковий випадок цього правила – два визначення
не повинні робити коло. «Обертання – це рух навколо осі». «Вісь – це пряма,
навколо якої йде обертання». Обидва визначення зробили коло, і залишилося
незрозумілим ні що таке вісь, ні що таке обертання.

3. Визначення не повинне бути заперечним, оскільки
заперечення завжди носить невизначений характер. Наприклад: «Кішка – не
собака». Зрозуміло, що не собака, але що таке кішка залишилося нез’ясованим.
Виключення: на заперечні поняття це правило не поширюється: «Безхазяйне майно –
це майно, що не має власника». Тут усе нормально.

4. Визначення повинне бути ясним, без метафор.
«Любов – це чародійство». Це метафора, а не визначення.

Щоб перевірити, чи правильно складене визначення,
достатньо поміняти його частину, що визначається та його частину, що визначає,
місцями. Якщо зміст не зміниться, значить, визначення складене правильно.
«Годинник – це вимірювальний прилад, що показує час» – «Вимірювальний прилад,
що показує час – це годинник». Зміст не змінився. Перед нами визначення. «Кінь
– це тварина» – «Тварина – це кінь». Зміст изменился. Це не визначення.

 

Поділ понять

Ми побачили, що визначення понять розкриває їх
зміст. Поділ же понять розкриває обсяг, тобто кількість класів предметів.

Логічна операція, що розкриває обсяг поняття,
називається поділом.

В операції поділу слід розрізняти поняття що
поділяється, обсяг якого слід розкрити, члени поділу –
співпідпорядковані види, на які поділяється поняття (вони ж – результат поділу)
і основа поділу – ознака, за якою здійснюється поділ. Про важливість
поділу говорить те, що він лежить у основі всякої класифікації.

Розрізняють поділ 1) за видозміною ознаки і 2)
дихотомічий поділ.

Поділ за видозміною ознаки. Основою поділу є ознака, при зміні якої
утворюються видові поняття, що входять до обсягу поняття, яке поділяється
(родового). Основою такого поділу можуть бути різні ознаки, це залежить від
мети поділу, від поставлених завдань. Але ці ознаки завжди повинні бути об’єктивними, інакше поділ буде
суб’єктивним.
Наприклад, якщо поділяти книги або кінофільми на цікаві та нецікаві, то це буде
суб’єктивний
поділ: для когось цікаві, а для когось – ні.

А тепер – правила поділу.

1. Поділ повинен бути співмірним – сума усіх видів
має рівнятися роду. З приводу першого правила прослухайте одне міркування: «Ті
студенти, які хочуть учитися, будуть добре вчитися і без усяких заохочень. Ті
студенти, які не хочуть учитися, все одно не будуть учитися, як їх не карай».
Тут порушене правило співмірності – цей поділ неповний. Є велика категорія
студентів, у яких немає стійкого ставлення до навчання, і тому система
заохочень, а, можливо й покарань, змогла б зіграти якусь роль. Правило
співмірності буде порушене і в тому випадку, якщо будуть указані зайві члени
поділу, тобто поняття, шо не є видами даного роду. Наприклад, якщо при
переліченні усіх фруктів, крім них, будуть указані ще й помідори, які, як
відомо, є овочами.

2. Поділ повинен здійснюватися лише за однією
основою. У процесі поділу вибрана ознака має лишатися однією й тією ж і не
підмінятися іншою ознакою. Приклад поділу за різними основами: «Населення
України поділяється на українців, жінок, шахтарів та інвалідів».

3. Члени поділу повинні виключати один другий. Це
правило тісно взаємопов’язане з попереднім. Якщо основи – різні, то і члени
поділу – видові поняття будуть знаходитися у відношенні часткового
співвпадіння, як у наведеному вище прикладі. Подібний же результат отримаємо,
якщо поділимо усіх студентів на заочників, першокурсників і спортсменів.

4. Поділ повинен бути безперервним. У процесі
поділу родового поняття треба переходити до найближчих видів, не пропускаючи
їх. Так, іноді буває, що види, у свою чергу, поділяються на підвиди. Тому не
можна переходити від поділу на види одного порядку до поділу на види наступного
порядку, наприклад, поділяти ссавців на хижаків, парнокопитних та коней. Якщо
перші два – це види першого порядку, то третє – це вид другого порядку (тут
пропущений вид першого порядку – непарнокопитні). Такий поділ позбавлений послідовності,
він називається стрибками у поділі.

Дихотомічний поділ, або дихотомія (від грецького «розтин на
дві частини») являє собою поділ обсягу поняття, що поділяється, на два
суперечних поняття. Якщо А – поняття, що поділяється, то членами поділу будуть
два поняття: В і не-В. Наприклад, усіх громадян можна поділити на повнолітніх
та неповнолітніх. Часто поділ на цьому не закінчується, негативне поняття можна
поділяти далі. Неповнолітніх можна поділити на тих, що досягли і не досягли 16
років (вони мають різний ступінь юридичної відповідальності), і, нарешті,
поділити останніх на тих, що досягли і не досягли 14 років. Але, у будь-якому
випадку, скільки б разів ми не роздрібнювали негативне поняття, кожний
дихотомічний поділ завжди охоплює весь обсяг поняття, що поділяється.

Дихотомічний поділ дуже корисний, коли треба
послідовно і швидко звузити коло предметів, щоб відшукати той, що цікавить нас,
наприклад, звузити коло підозрюваних. Але інколи дихотомічний поділ лише
ускладнює завдання. Наприклад, нам треба класифікувати домашніх тварин.
Припустимо, нам більше всього подобаються коти, тоді ми поділяємо усіх тварин
на дві групи: «коти» и «не-коти». Далі, «не-котів» поділяємо на «собак» и
«не-собак», при цьому не забуваючи, щоо «котів» уже виділили раніше. Чи буде
раціональним такий поділ Звичайно, ні. Простіше одразу поділити домашніх
тварин на котів, собак, хом’ячків і т. д.

Операції з класами

За допомогою логічних операцій з двох або кількох
класів можуть бути утворені нові класи. До цих операцій належать:

1. Операція об’єнання класів (додавання).
Записується вона так: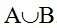. Об’єднувати можна класи, що
знаходяться у будь-яких відношеннях один з одним:

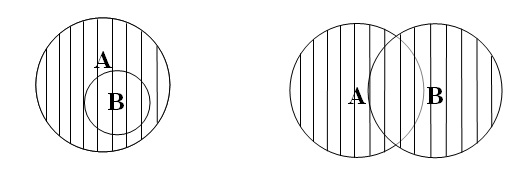
(У першому випадку А – студенти, В –
першокурсники, у другому випадку А – студенти, В – спортсмени).

2. Операція віднімання класів дає клас,
який виключає елементи класів, що віднімаються.

Наприклад, якщо від класу «студенти» відняти клас
«спортсмени», то залишаться студенти-неспортсмени.

 

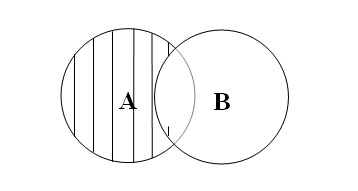
3. Операція перетину класів (множення)
полягає у відшуканні елементів, спільних для двох або кількох класів (множин).
У нашому випадку це будуть студенти-спортсмени:

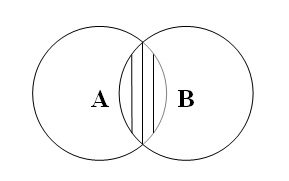
Операція перетину класів записується за допомогою
знака множення: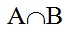 

Множина, отримана у результаті множення
називається, також, як і в математиці, добутком. При множенні несумісних
понять, наприклад, «слідчі» та «адвокати», виходить пустий (нульовий) класс.

4. Утворення доповнення (заперечення).
Доповненням до класу А називається клас не-А (А’), який
при додаванні до А утворює універсальний класс (позначається знаком 1). Щоб
утворити доповнення, треба з універсального класу виключити клас А:

1 – А = А‘

Для цього ми повинні визначити спочатку, до якого
універсального класу належить даний клас. Наприклад, клас бухгалтерів належить
до універсального класу економістів. Тепер, якщо виключити з класу економістів
клас бухгалтерів, то ми отримуємо множину економістів-небухгалтерів. У своїй
сумі обидва поняття утворюють універсальний клас економістів.

Щоб кожного разу не звертатися до кіл, треба
запам’ятати деякі закони операцій над множинами.

 

Рекомендована література

1. Бочаров В.А., Маркин В.И. Основы логики. – М.:
Изд-во “Инфра-М”, 1997.- 296с.

2. Войшвилло Е.К. Понятие как форма мышления. –
М.: Изд-во, МГУ, 1989.

3. Горский Д.П., Ивин А.А, Никифоров А.Л. Краткий
словарь по логике. – М., 1991.

4. Грядовой Д.И., Малахов В.П. Логика для юриста.
– М., 1998.

5. Иванов Е.А. Логика. – М., 2001.

6. Івін О.А. Логіка. – К.,1996.

7. Ивлев Ю.В. Логика. – М.: “Наука”, 2002.

8. Кириллов В.И., Старченко А.А. Логика: Учебник
для юридических вузов. – М., 1995.

9. Литвак М.Е. Как узнать и изменить свою судьбу.
– Ростов-на – Дону: Феникс. 2002.

10. Мельников В.Н. Логические задачи. – К. – Одесса, 1989.

11. Сборник упражнений по логике. – Минск, 1990.

12. Хоменко В. І. Логіка для юристів. – К.,
2001.